标准规范下载简介和预览
在线阅读
中华人民共和国国家标准化指导性技术文件
室内照明计算基本方法
Calculations for interior lighting basic method
GB/Z 26213-2010
发布日期:2011年1月14日
实施日期:2011年6月1日
前言
本指导性技术文件等同翻译CIE 40-1978。
为便于使用,本指导性技术文件做了下列编辑性修改:
a) “本技术报告”一词改为“本指导性技术文件”;
b) 用小数点“.”代替作为小数点的“,”;
c) 删除CIE 40-1978的前言。
本指导性技术文件由中国轻工业联合会提出。
本指导性技术文件由全国照明电器标准化技术委员会(SAC/TC 224)归口。
本指导性技术文件起草单位:国家电光源质量监督检验中心(北京)、中国质量认证中心、广东东松三雄电器有限公司、生辉照明电器(浙江)有限公司、霍尼韦尔朗能电器系统技术(广东)有限公司、东莞乐域塑胶电子制品有限公司、北京电光源研究所。
本指导性技术文件主要起草人:华树明、邢合萍、张宇涛、沈锦祥、付宝成、李维升、劳应海、赵雅盛、江姗、段彦芳。
本指导性技术文件仅供参考。有关对本指导性技术文件的建议和意见,向国务院标准化行政主管部门反映。
1 总则
本指导性技术文件提出了一个基本方法,是一种不需要依靠标准灯具光分布,并且不受限于灯具的常规安装的方法。
此方法被称为“基本方法”,原因在于它作为应用方法的基础。
此方法可应用在如下领域:
a)室内环境是一个长方形的平行六面体;
b)工作面可假定为某种材料的平面,并被认为是房屋的一个内表面;
c)房间表面均匀反射并且符合朗伯定律,天花板反射比为R1,中楣反射比为R2(定义为在天花板与灯具间垂直面的部分),墙面反射比为R3(定义为在灯具平面与工作面之间的垂直表面),R4为工作表面反射比;
d)如果灯具围绕它们的垂直轴线旋转,工作表面的直接照射光通量并不发生显著改变。
2 工作面F4的直接照射光通量
为定义工作面的直接照射光通量,假设灯具发射的光是锥形的,有与灯具的垂直轴线重合的轴线,并可以表达成锥形的不含常数项的4次多项式立体角函数。
多项式中,通过选择属于不同灯具的特定系数,给出与四个立体角区域π/2、π、3π/2、2π实际积分光通量相同的精确值。在提出的方法中,这4个区域的光通量FC1、FC2、FC3和FC4描述了下照光的分布情况,F为灯具的总光输出(上照光及下照光)。
在这些条件中,长方形获得的来自于其某个角垂直上方的对称点光源光通量(Fu)是光通量FC1、FC2、FC3、FC4的线性函数。
权重因数GM1、GM2、 GM3、GM4是长方形各边长与灯具到长方形高度距离的比值函数X/H和Y/H(见图1)。这些因数乘以1000后,由表Ⅰ.1~表Ⅰ.6给出。
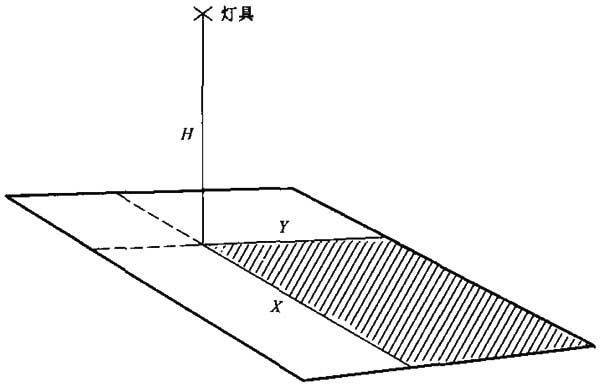
图1
例如:假设X=2.25m,Y=3.30m H=1.5m
X/H=1.5和Y/H=2.2
从表Ⅰ.4查到如下数据:
GM1=—12;GM2=218;GM3=47;GM4=—4
这些数值以1000倍给出,所以:
Fu=(—12FC1+218FC2+47FC3—4FC4)/1000
如上式操作4次,对于给定灯具和安装环境的房间,可以得出工作面接收的直接照射光通量(Fu)等于:
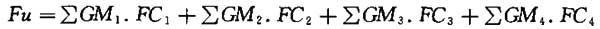
例如:假定房间A=3m,B=4.5m,H=1.5m
在天花板安装的灯具安装位置如下:
X=2.25m,为距离房屋长边的距离;
Y=3.30m,为距离房屋短边的距离。
考虑四个矩形的数据对(X/H;Y/H)分别为:
(1.5;2.2),(0.5;2.2),(0.8;1.5),(0.5;0.8)。
查阅表Ⅰ.4,表Ⅰ.2,表Ⅰ.2和表Ⅰ.1:

由此,如下:
Fu=(591FC1+253FC2+101FC3—13FC4)/1000
直接光通量F4是每个安装灯具的光通量之和。
3 互反射
相互反射的计算是在假设总照度(直接照度通过反射照度而增加)在整个天花板-中楣、墙面、工作面均匀分布的条件下进行的。
在这些条件下,通常尺寸的室内空间,互反射实际上仅仅由灯具的悬挂因数J与由图2定义的房间指数K的相互关系有关,见下面公式。
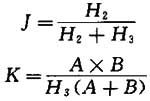
A和B是房屋侧边长,H3是灯具平面与工作面的距离,H2是中楣高度(天花板与灯具面的距离)。
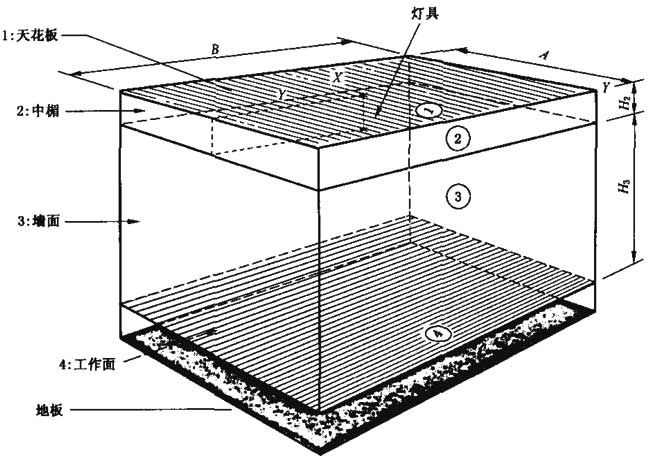
图2
4 照度的计算
如果(NM)是房屋内的灯具数量;
F是一个灯具的全部光输出值(上照光与下照光);
FC4是灯具下照光通量;
F4是全部灯具直接照射到工作面上的光通量;
A和B是房屋的侧边长。
天花板上的平均照度E1,墙面上的平均照度E3、工作面上的平均照度E4可通过下面F、FC、F4的线性函数计算:
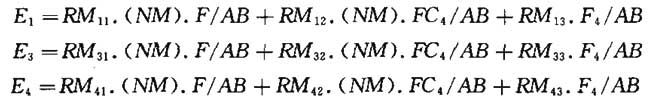
权重因子RM在表Ⅱ.1~表Ⅱ.24查阅。
例如:设J=0;K=0.6且R1,R3,R4=873
查阅表Ⅱ.1第一行
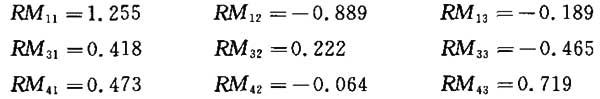
如A和B的单位是米,则照度单位是勒克斯。
5 灯具光通量的计算
如果E1表示天花板和中楣上的平均照度;
E3表示墙面上的平均照度;
E4表示工作面上的平均照度;
AB表示工作面的面积;
(NM).F表示总光通量;
(NM).FC4表示下半球光通量;
F4表示灯具直接向工作面发出的光通量,
后三个数值可通过下列线性公式计算:
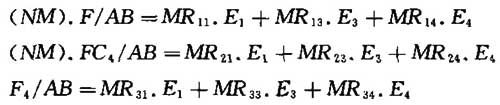
系数MR可在表Ⅲ.1~表Ⅲ.24中查到。
例如:设J=0;K=0.6且R1,R3,R4=873
下列系数可在表Ⅲ.1的第一行查到:
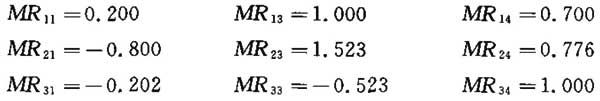
表Ⅰ
表Ⅰ.1


单个灯具垂直位于边为X/H和Y/H的矩形一角上方的几何多重因数。
该值以1/1000表示。
表Ⅰ.2
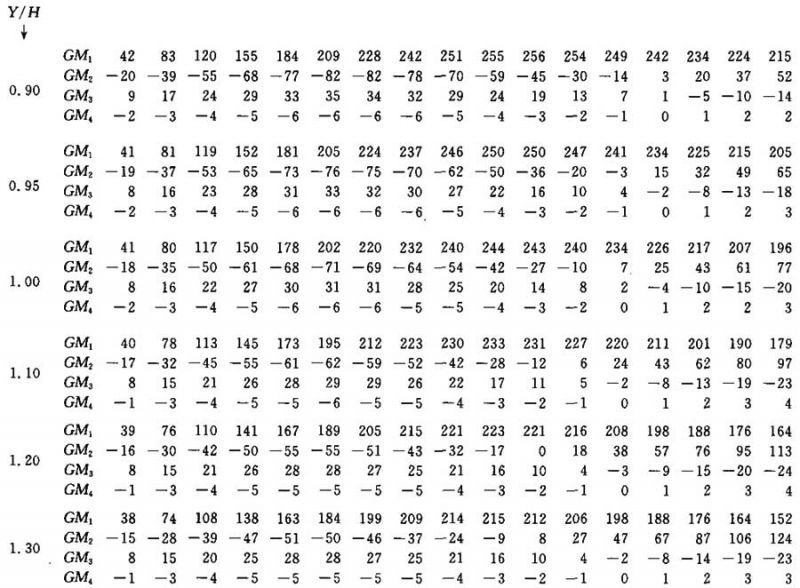
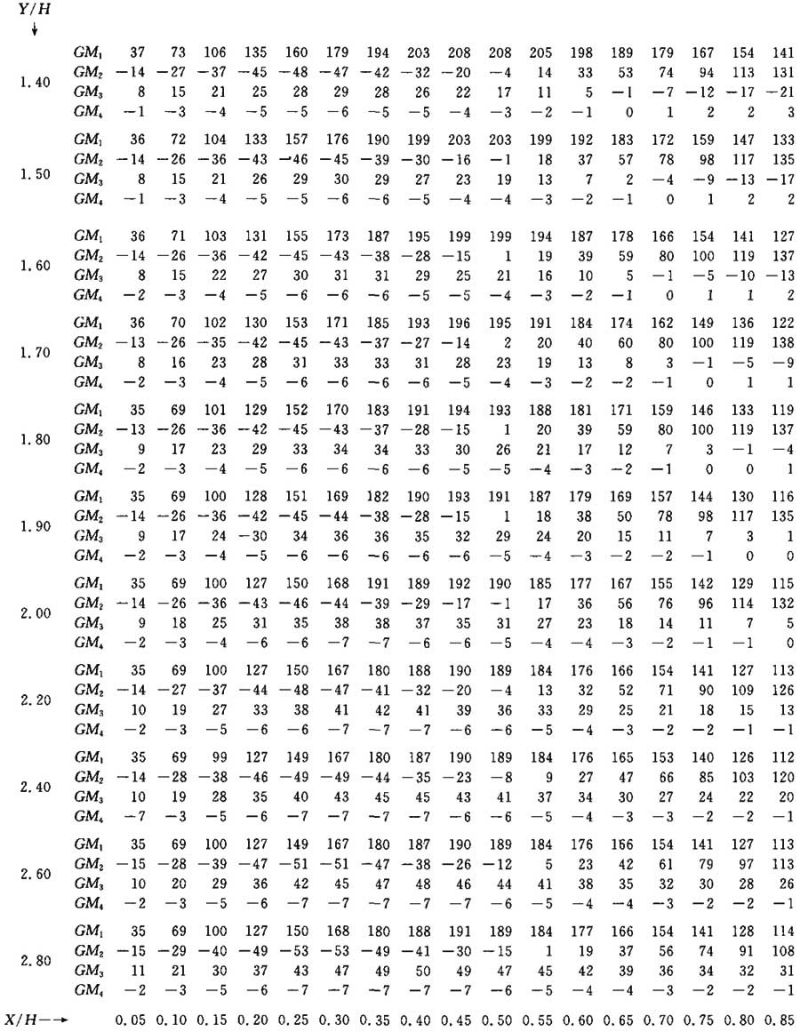
单个灯具垂直位于边为X/H和Y/H的矩形一角上方的几何多重因数。
该值以1/1000表示。
表Ⅰ.3
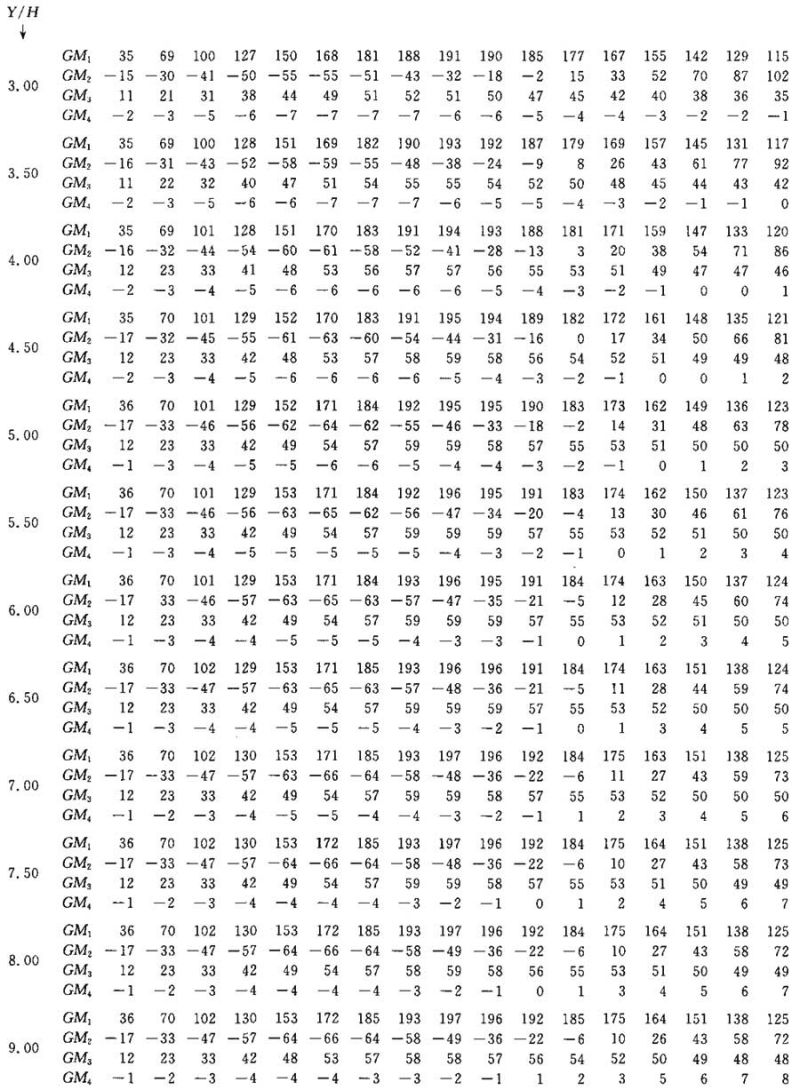

单个灯具垂直位于边为X/H和Y/H的矩形一角上方的几何多重因数。
该值以1/1000表示。
表Ⅰ.4


单个灯具垂直位于边为X/H和Y/H的矩形一角上方的几何多重因数。
该值以1/1000表示。
表Ⅰ.5

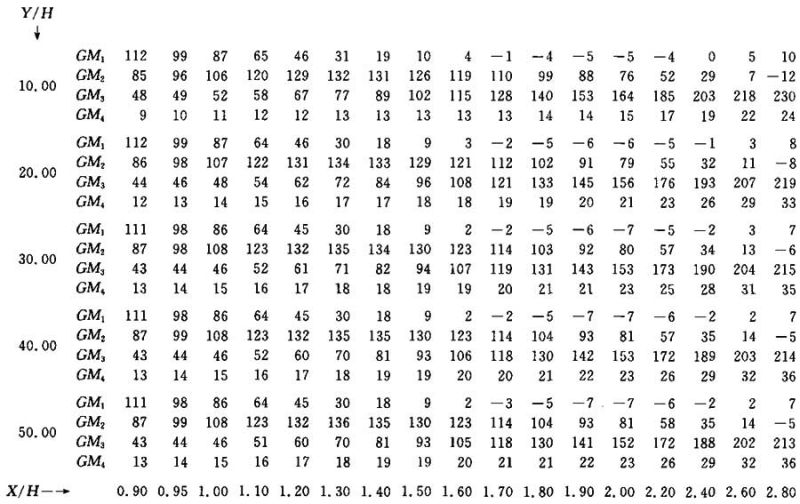
单个灯具垂直位于边为X/H和Y/H的矩形一角上方的几何多重因数。
该值以1/1000表示。
表Ⅰ.6


单个灯具垂直位于边为X/H和Y/H的矩形一角上方的几何多重因数。
该值以1/1000表示。
表Ⅱ
照度E1、E3和E4的计算系数表
表Ⅱ.1
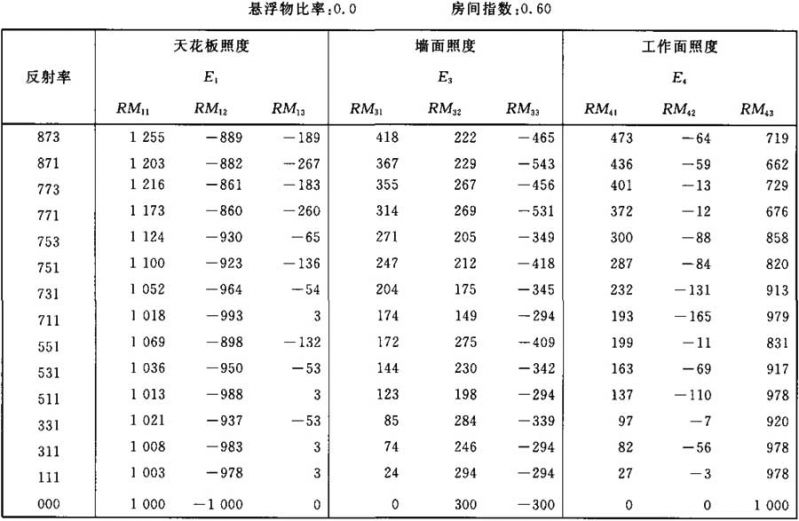
照度E1、E3和E4的计算系数表
表Ⅱ.2
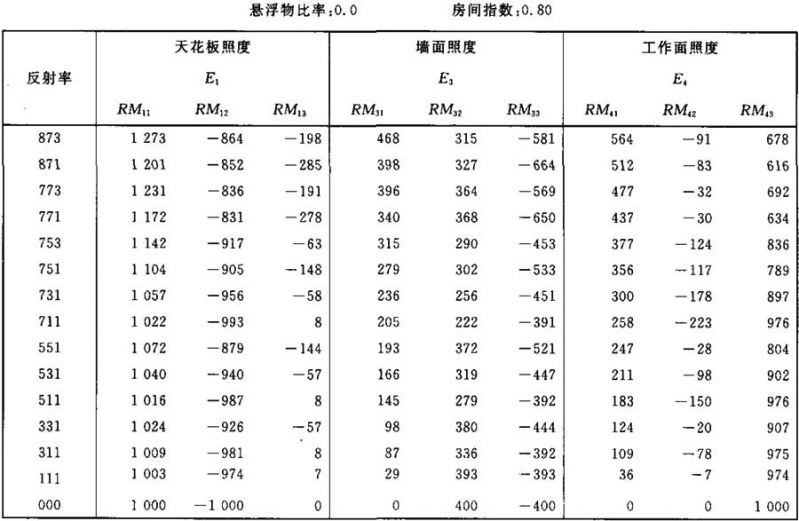
照度E1、E3和E4的计算系数表
表Ⅱ.3
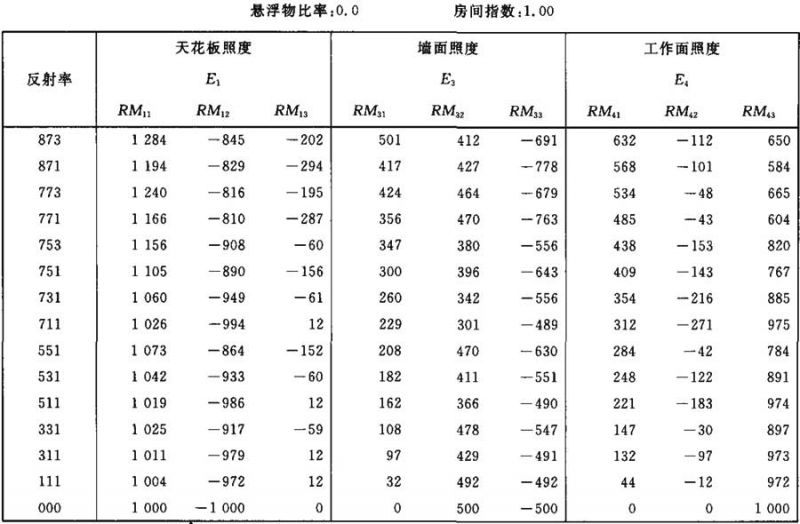
照度E1、E3和E4的计算系数表
表Ⅱ.4
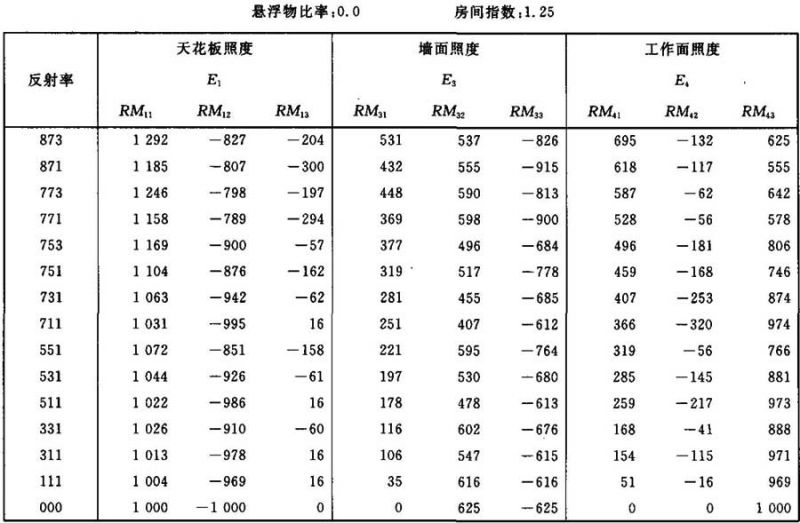
照度E1、E3和E4的计算系数表
表Ⅱ.5
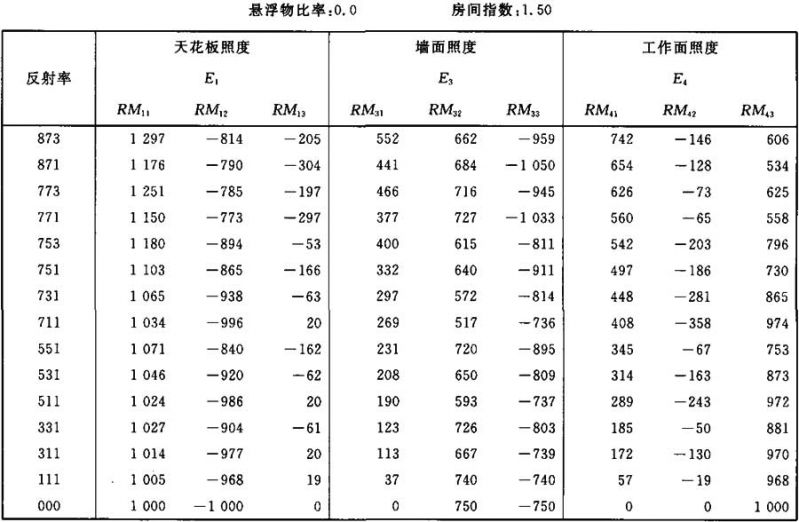
照度E1、E3和E4的计算系数表
表Ⅱ.6
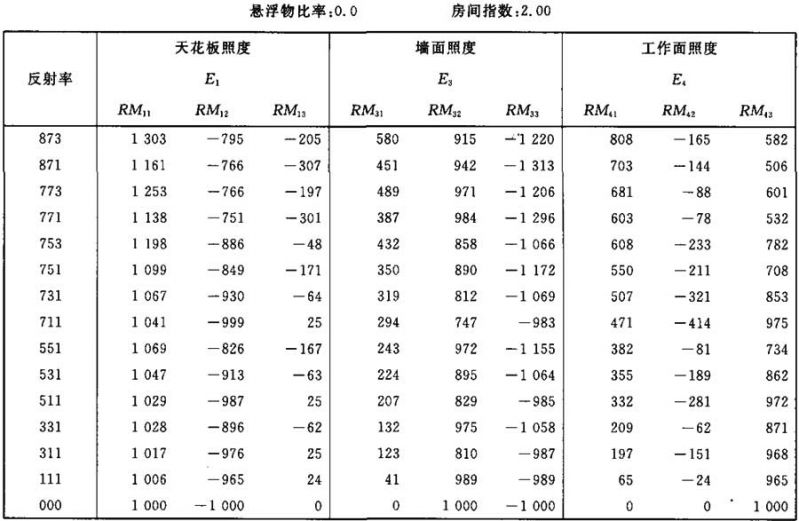
照度E1、E3和E4的计算系数表
表Ⅱ.7
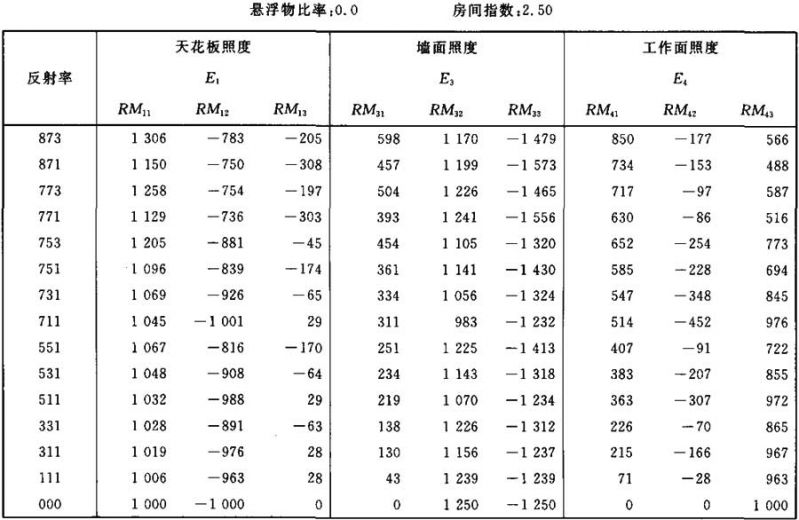
照度E1、E3和E4的计算系数表
表Ⅱ.8
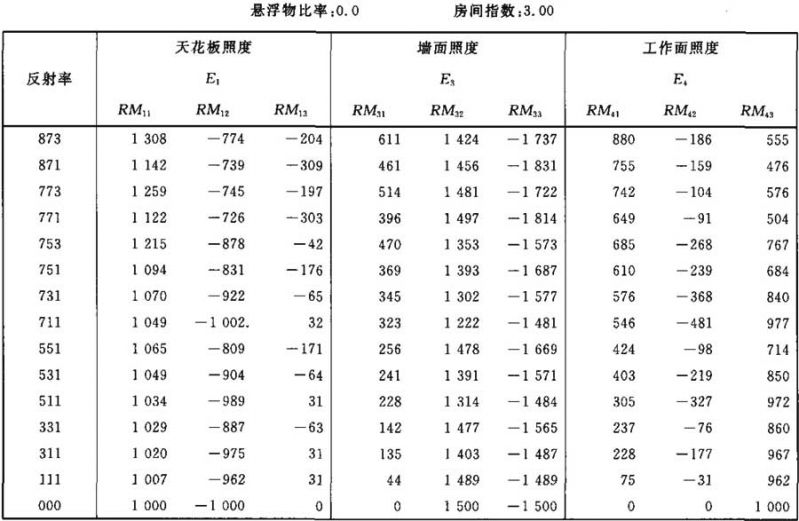
照度E1、E3和E4的计算系数表
表Ⅱ.9
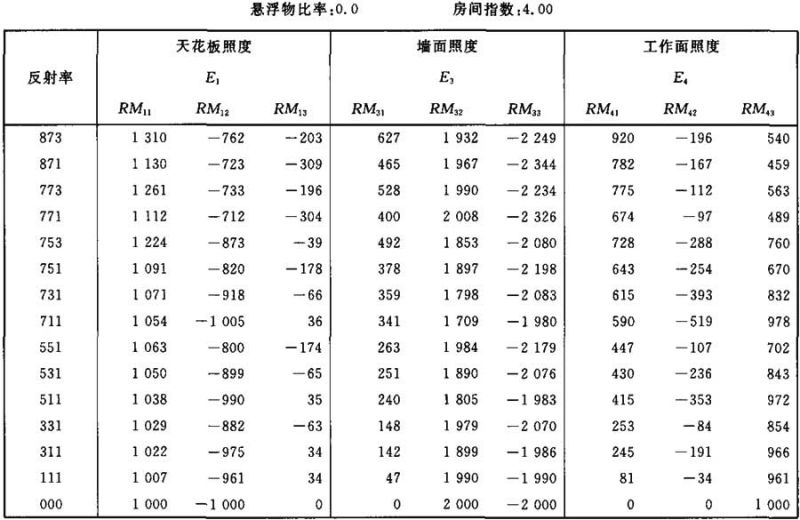
照度E1、E3和E4的计算系数表
表Ⅱ.10
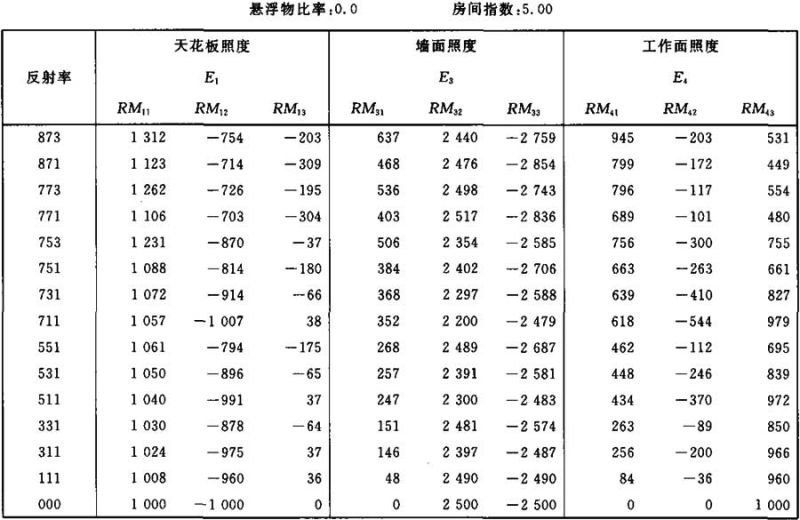
照度E1、E3和E4的计算系数表
表Ⅱ.11
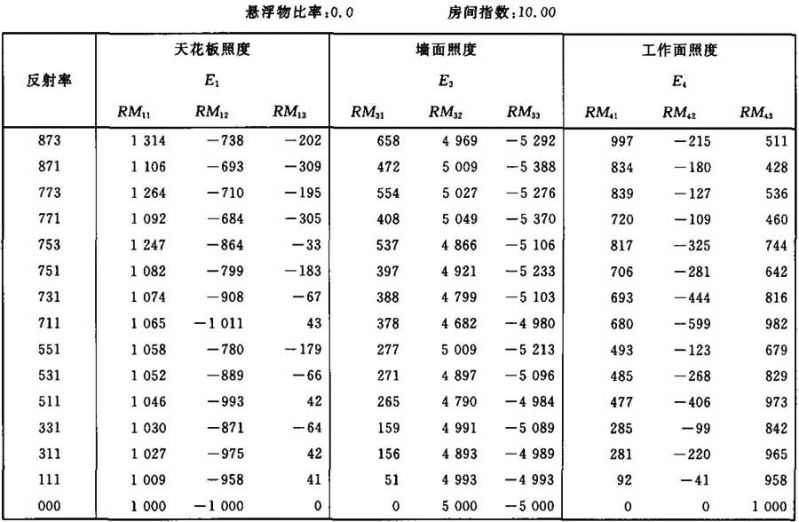
照度E1、E3和E4的计算系数表
表Ⅱ.12

照度E1、E3和E4的计算系数表
表Ⅱ.13
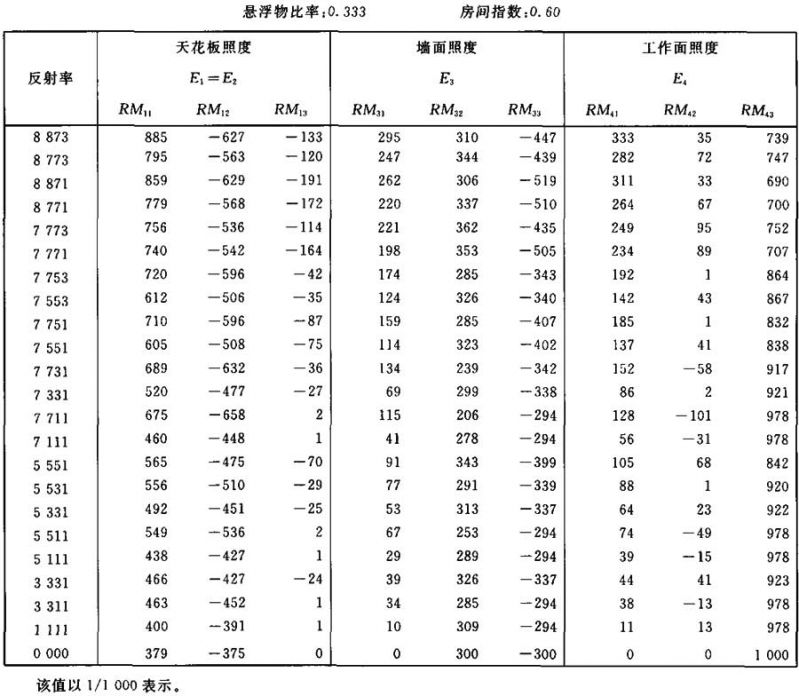
照度E1、E3和E4的计算系数表
表Ⅱ.14

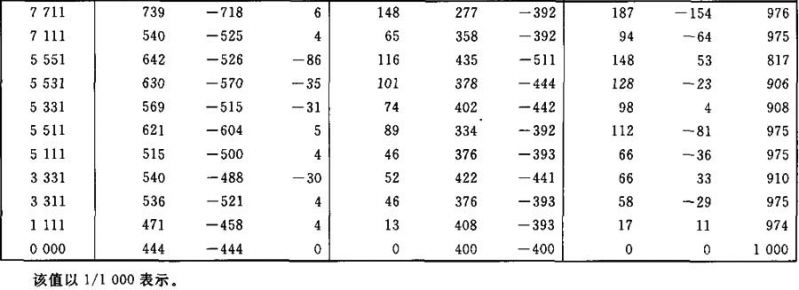
照度E1、E3和E4的计算系数表
表Ⅱ.15
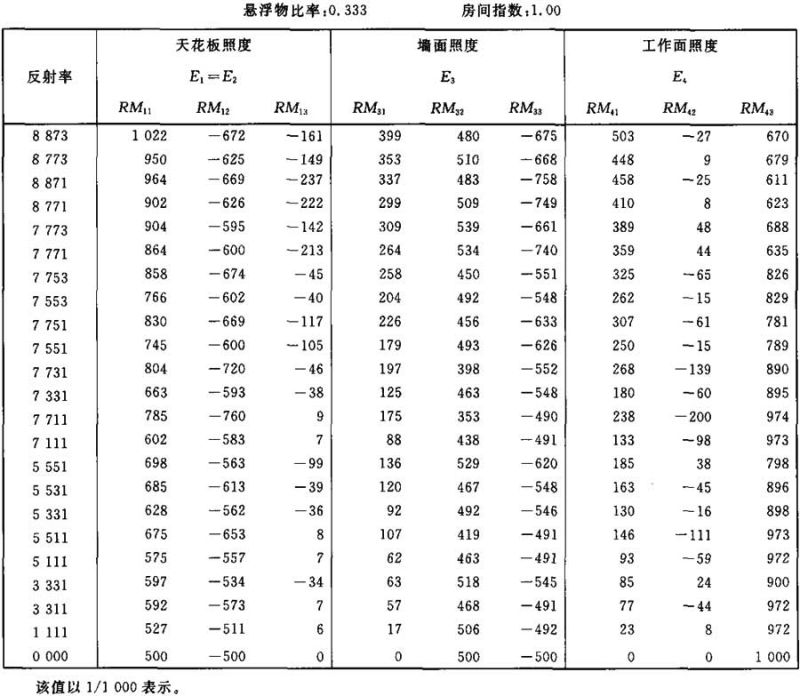
照度E1、E3和E4的计算系数表
表Ⅱ.16
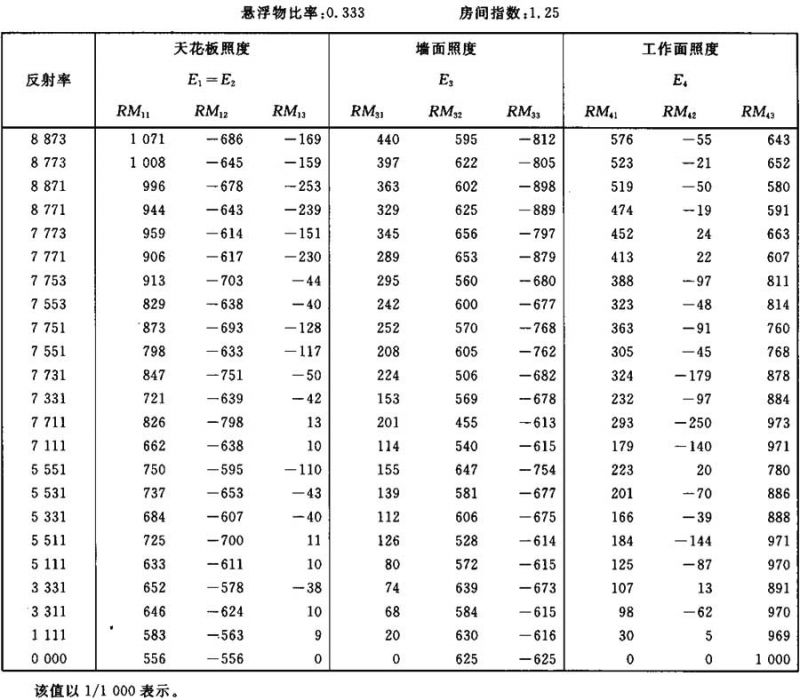
照度E1、E3和E4的计算系数表
表Ⅱ.17
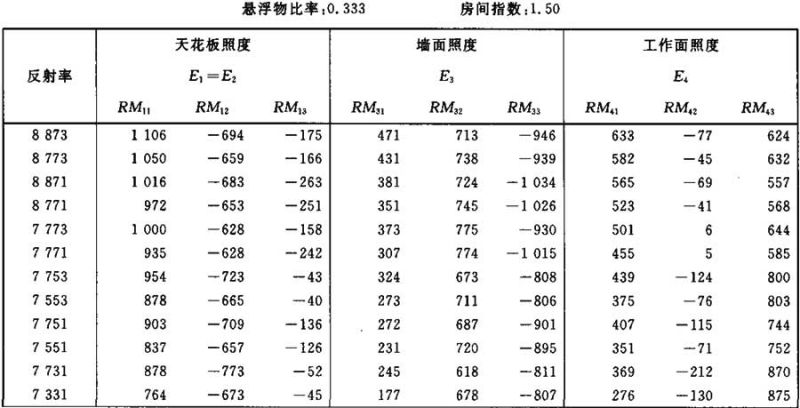
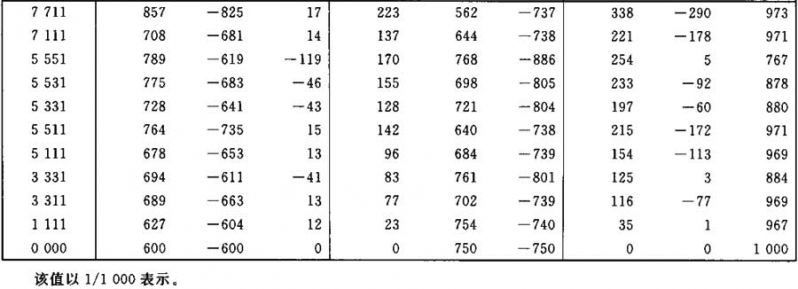
照度E1、E3和E4的计算系数表
表Ⅱ.18
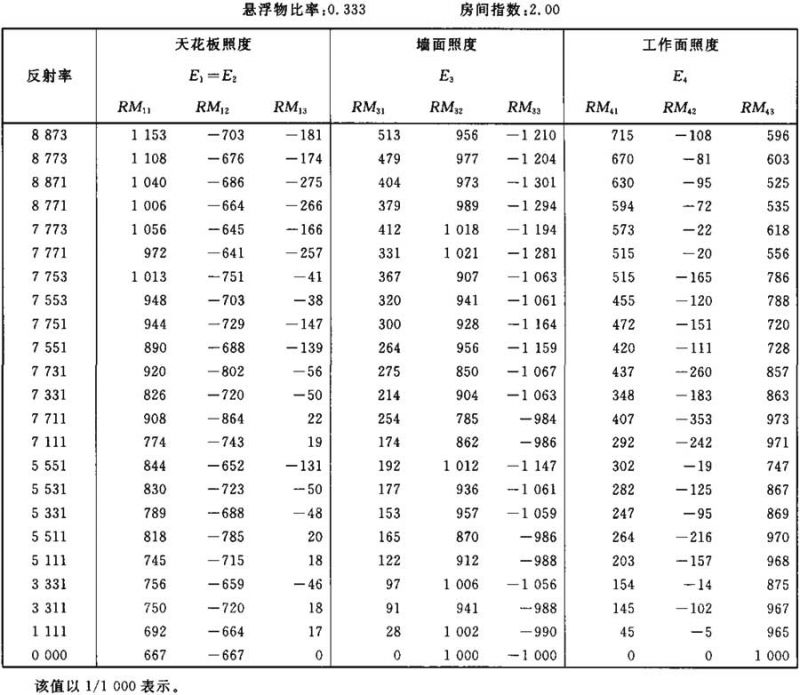
照度E1、E3和E4的计算系数表
表Ⅱ.19
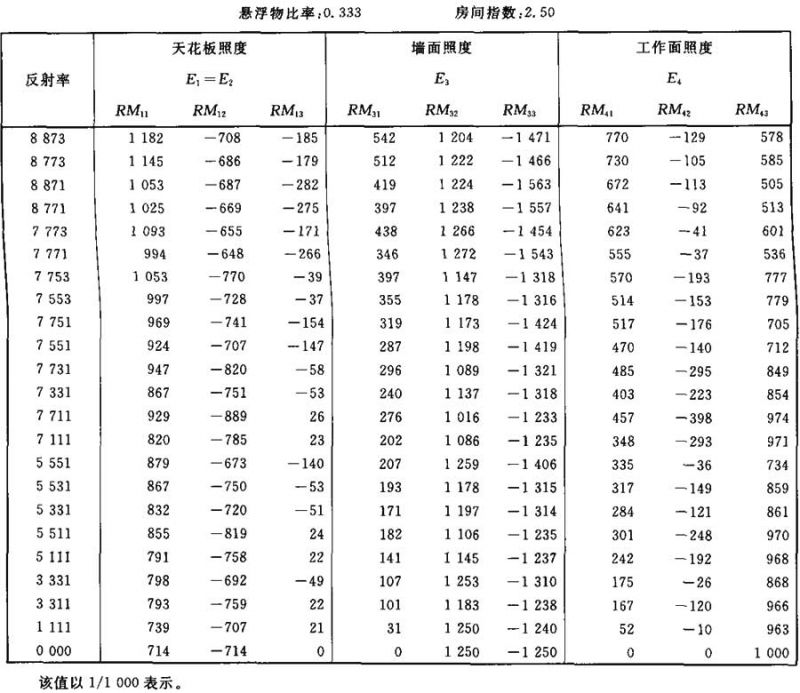
照度E1、E3和E4的计算系数表
表Ⅱ.20
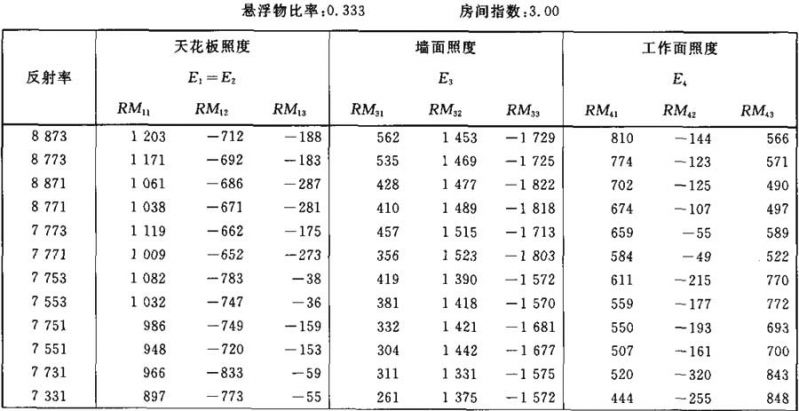
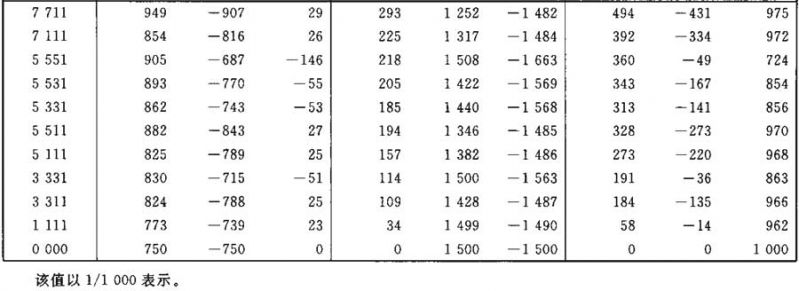
照度E1、E3和E4的计算系数表
表Ⅱ.21
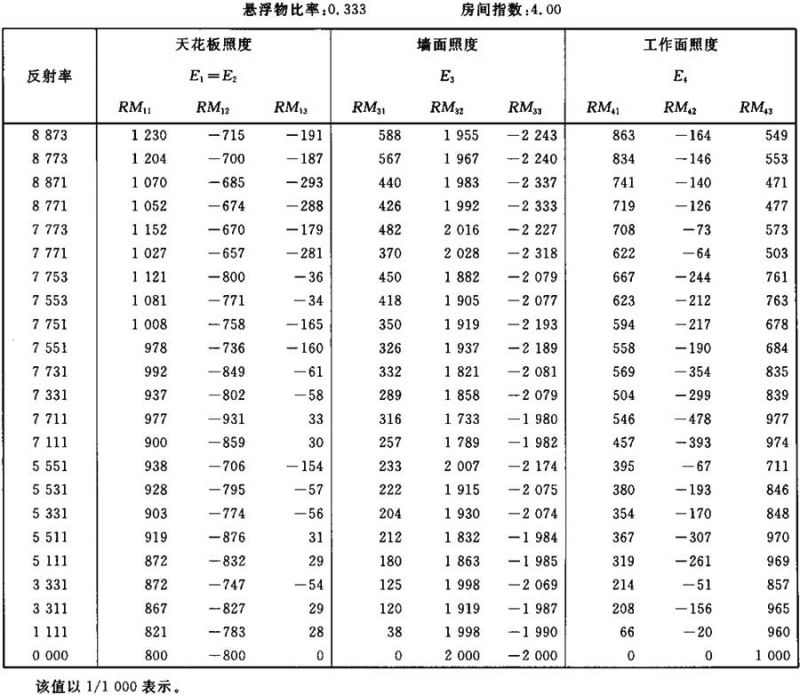
照度E1、E3和E4的计算系数表
表Ⅱ.22
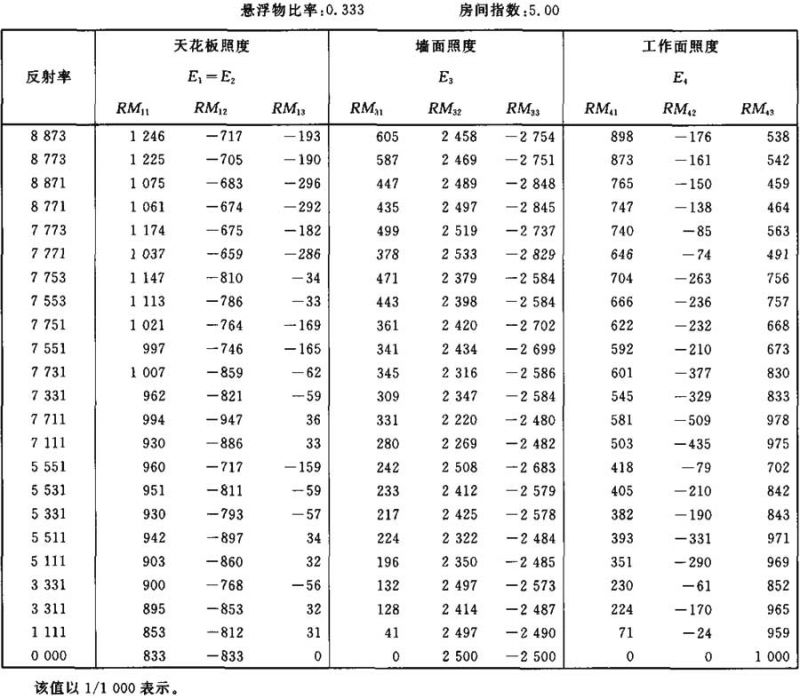
照度E1、E3和E4的计算系数表
表Ⅱ.23
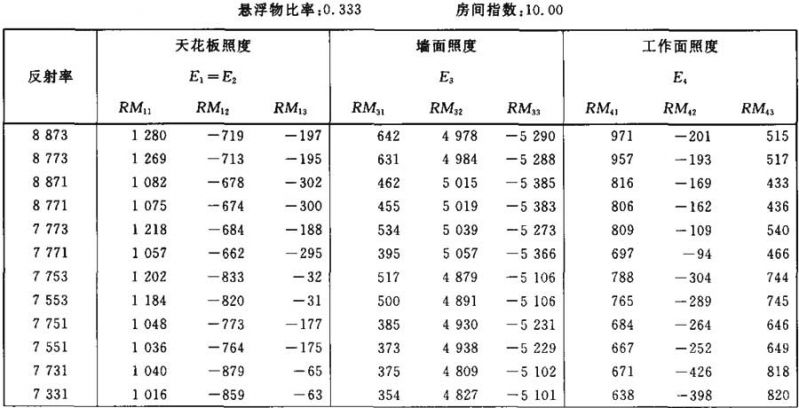
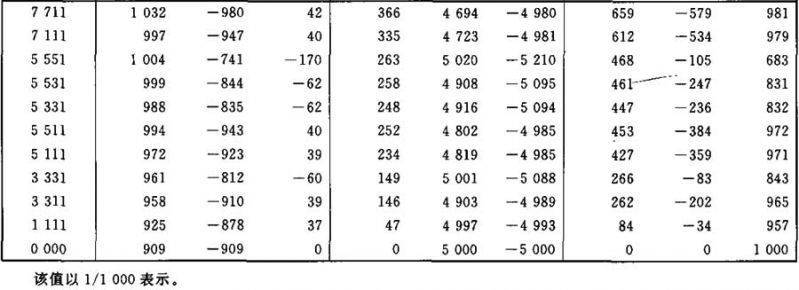
照度E1、E3和E4的计算系数表
表Ⅱ.24
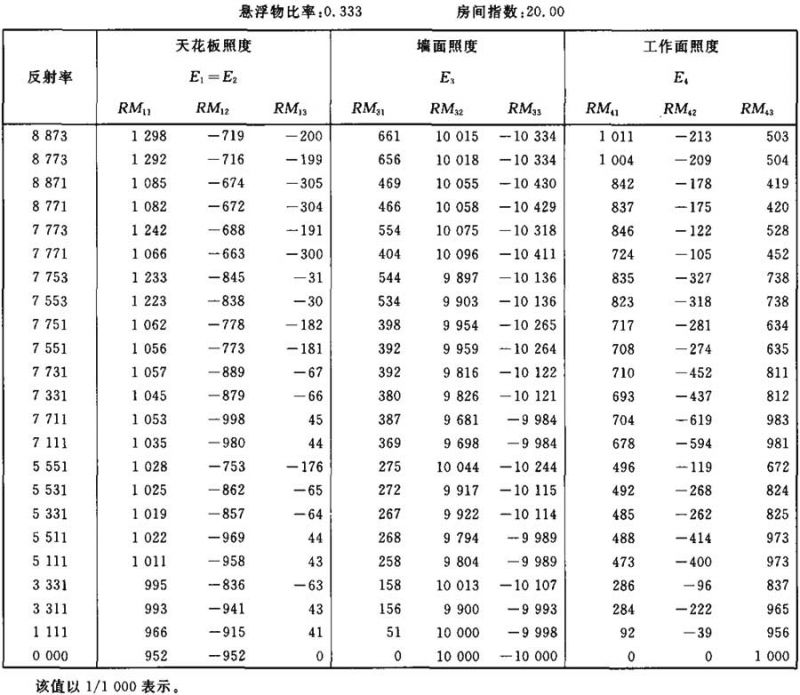
表Ⅲ
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.1
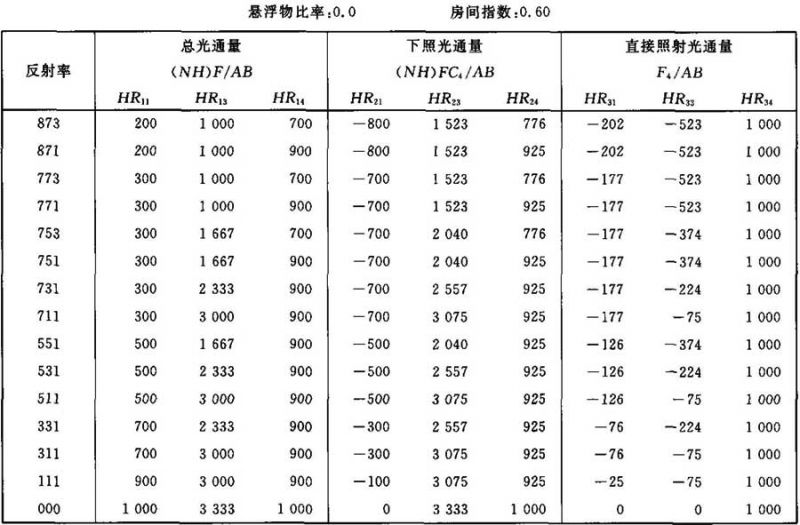
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.2
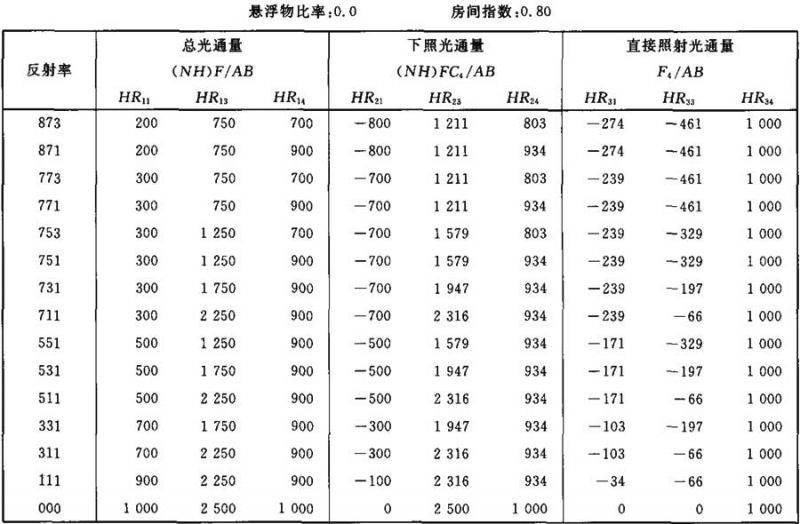
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.3
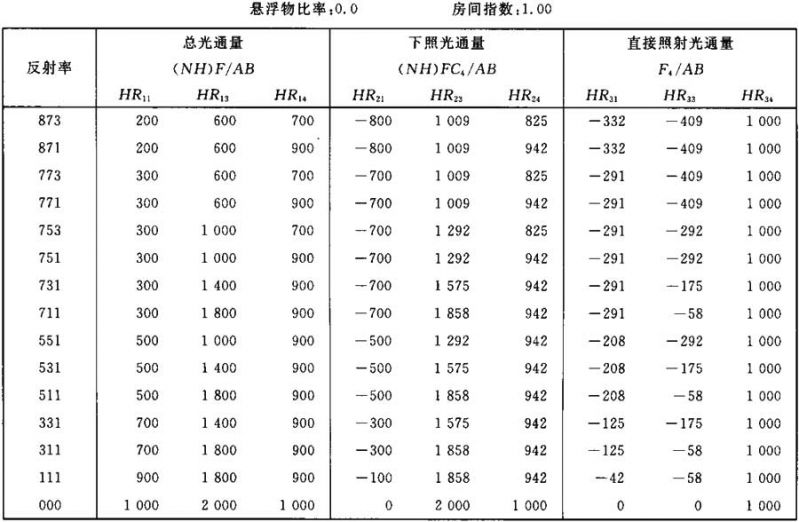
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.4
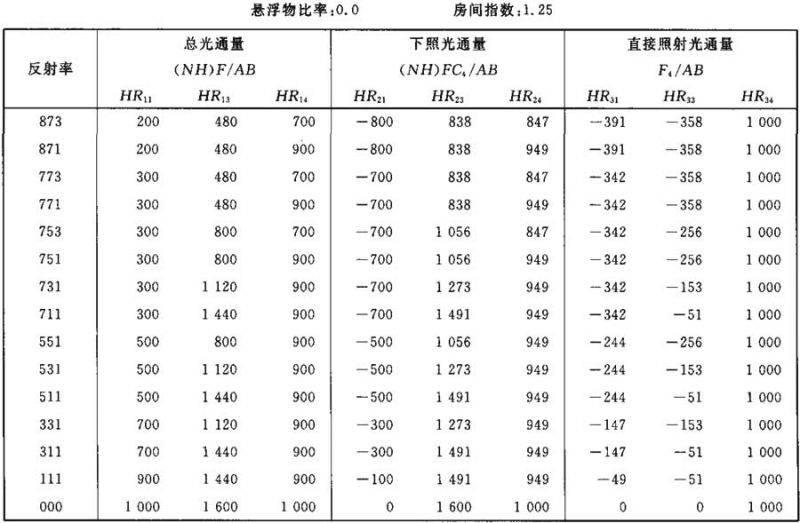
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.5
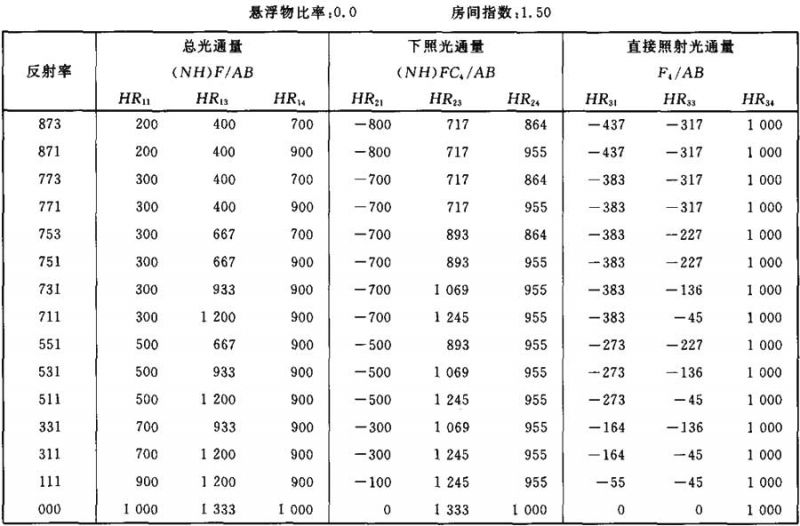
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.6
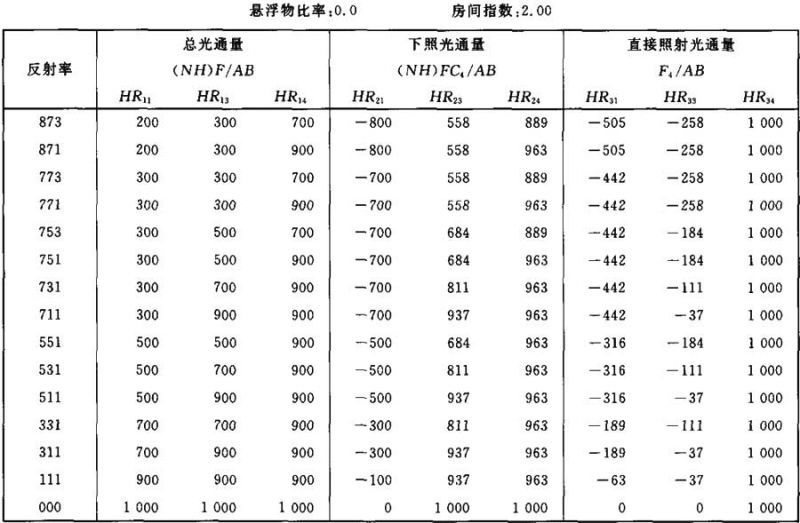
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.7
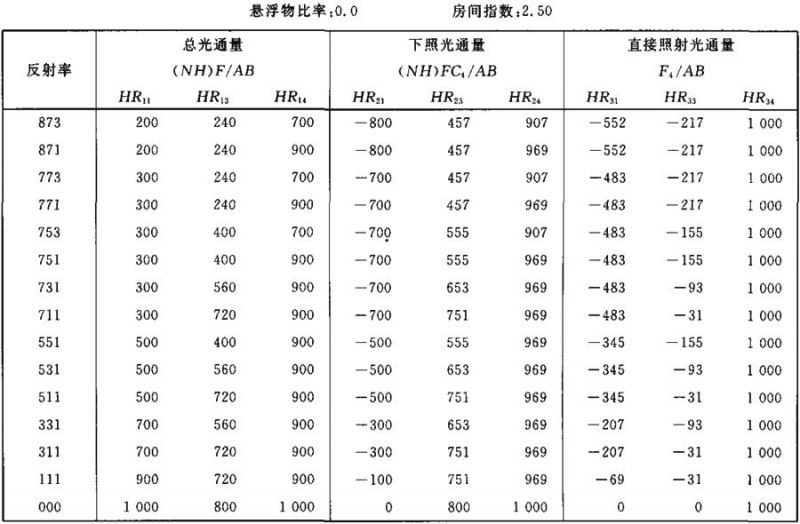
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.8
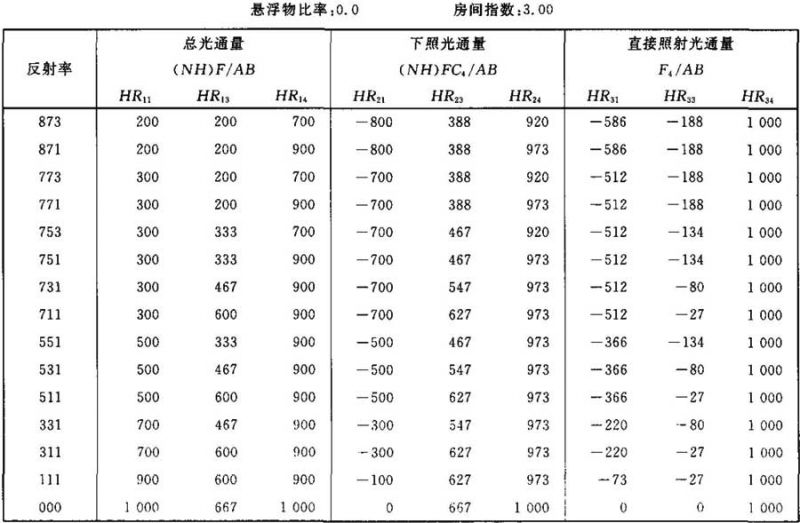
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.9
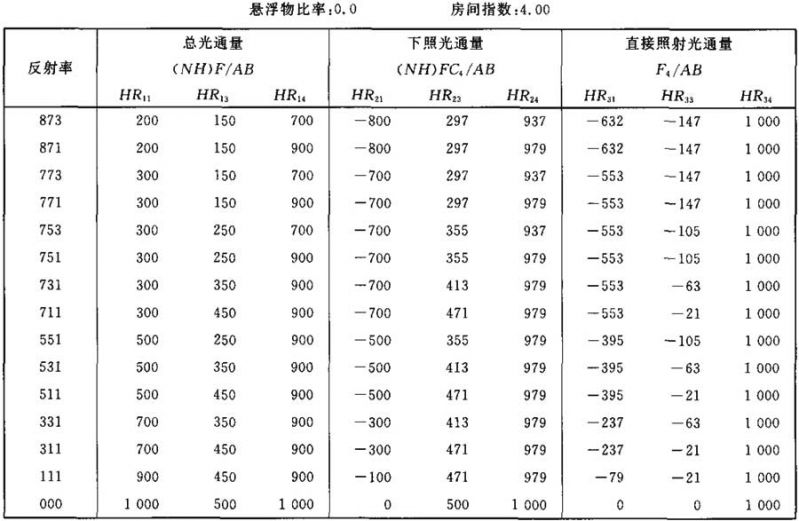
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.10
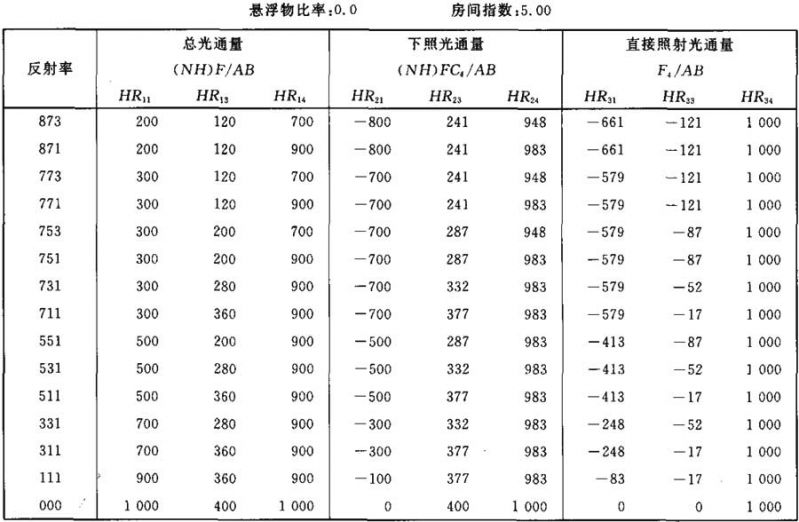
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.11
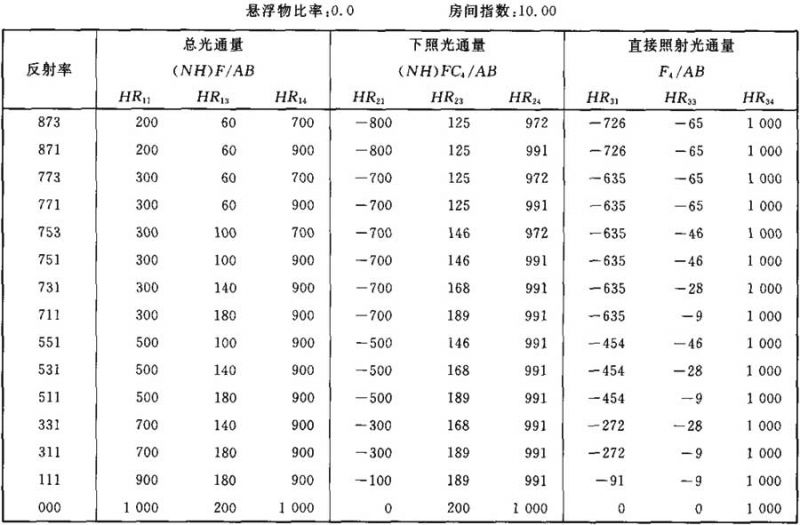
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.12
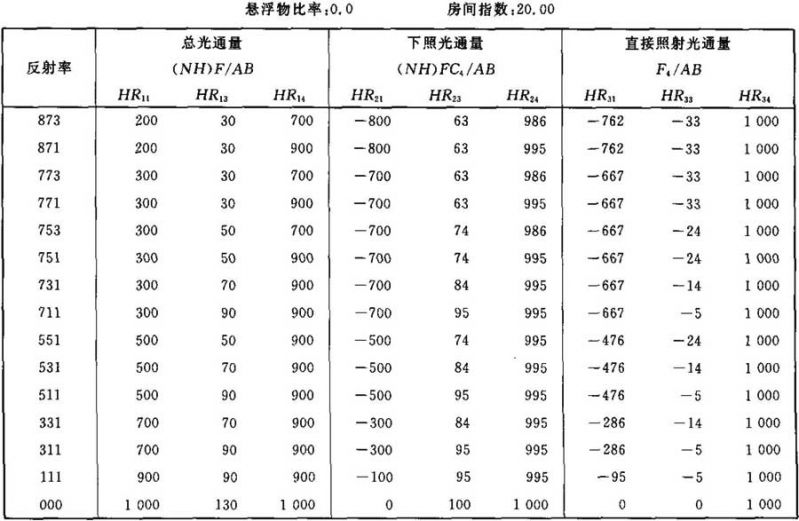
光通量值(NH)F/AB (NH)FC4/AB F4/AB的计算系数表
表Ⅲ.13
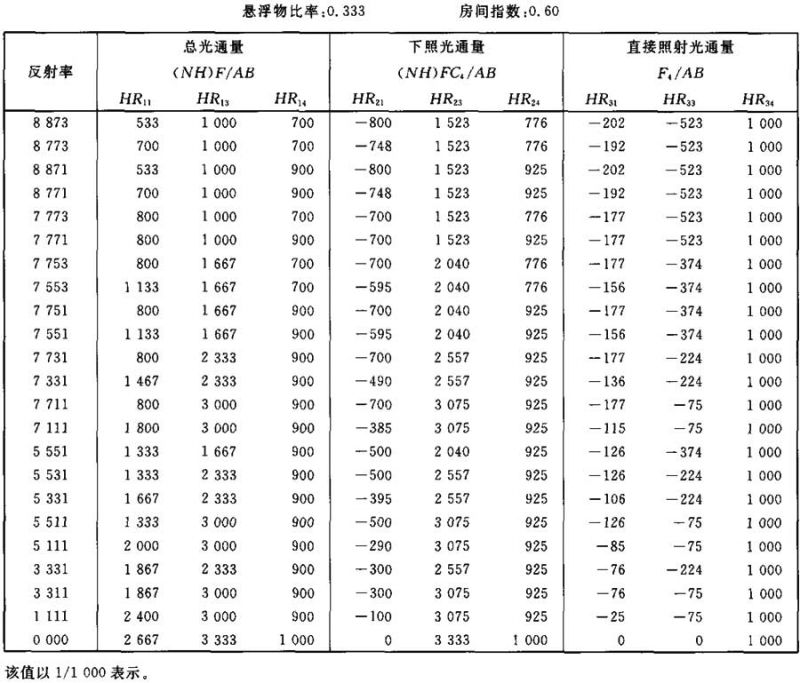
表Ⅲ.14
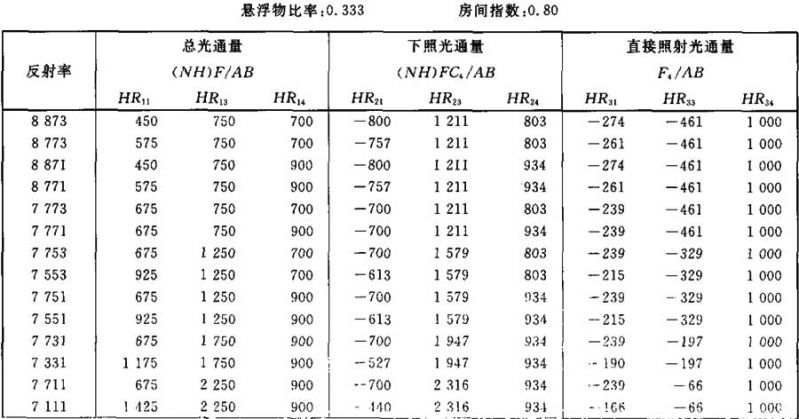
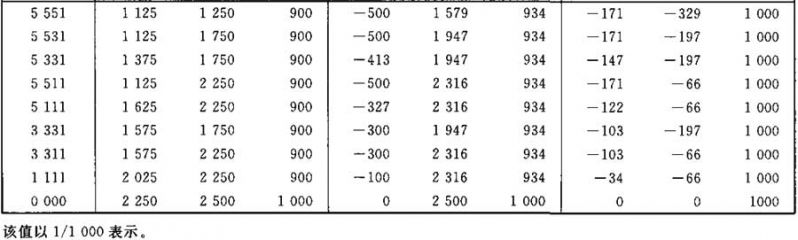
表Ⅲ.15
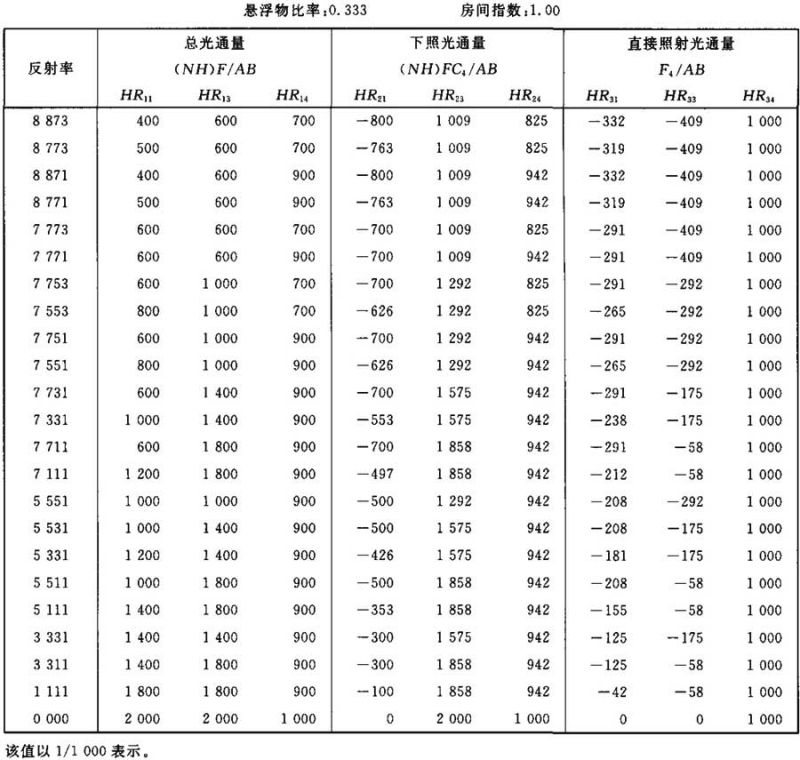
表Ⅲ.16
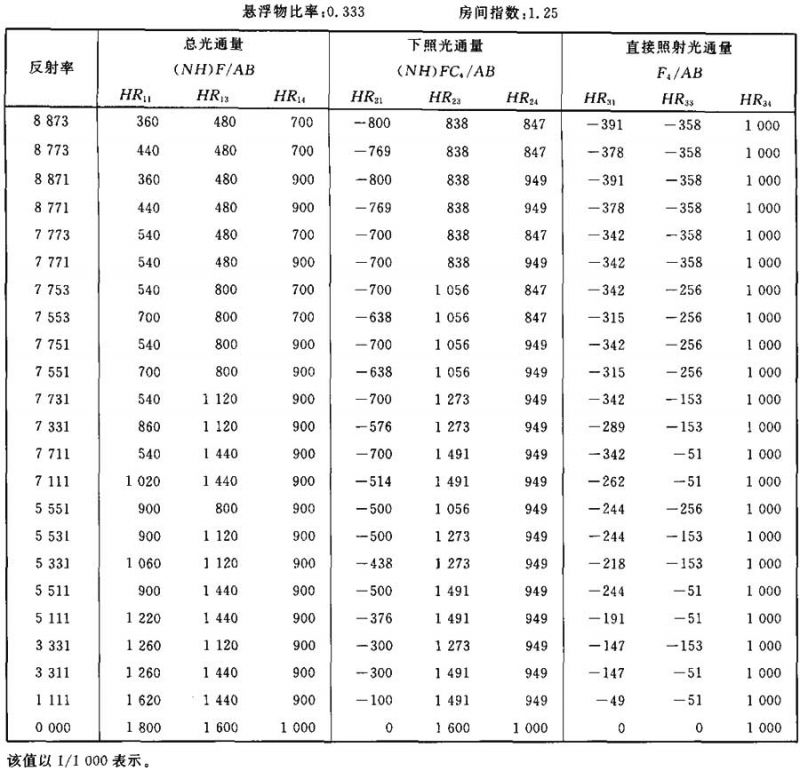
表Ⅲ.17
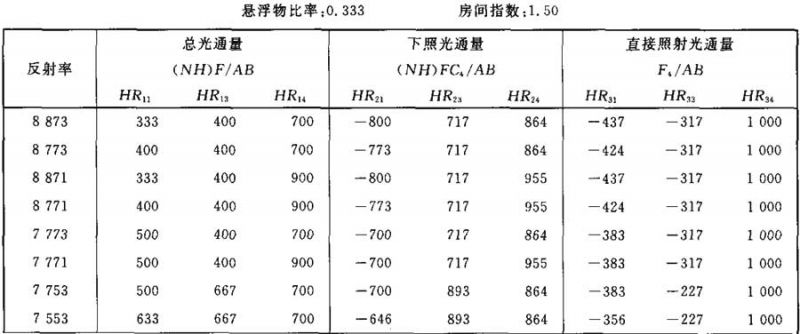
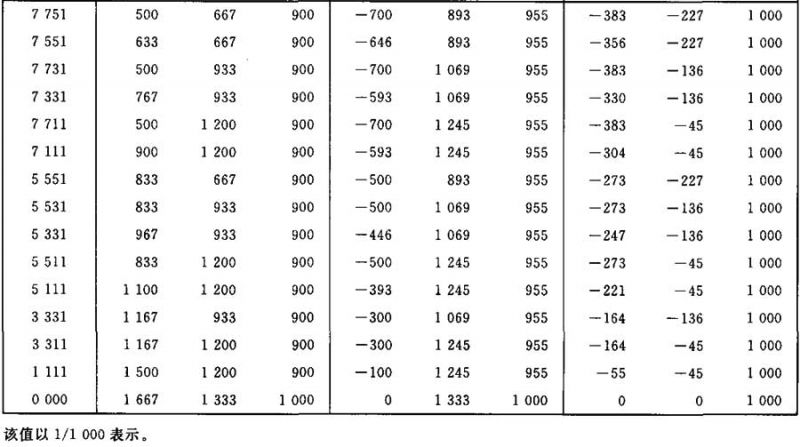
表Ⅲ.18
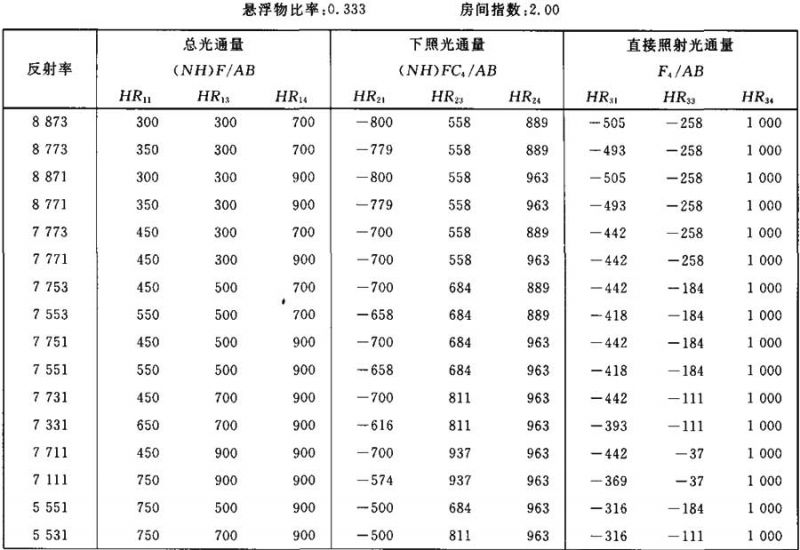
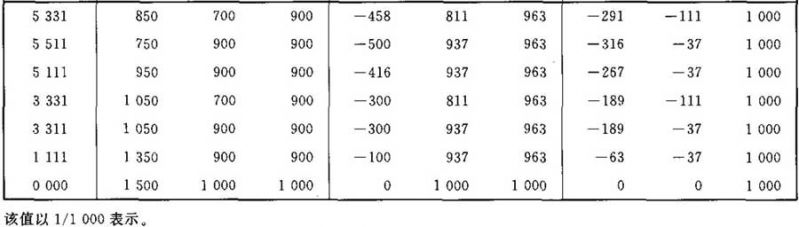
表Ⅲ.19
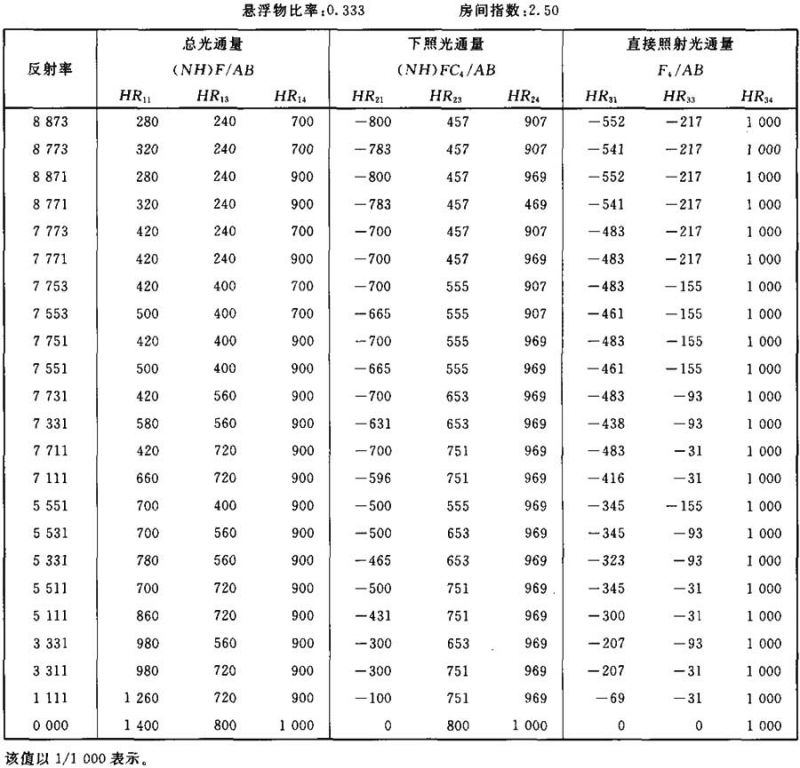
表Ⅲ.20
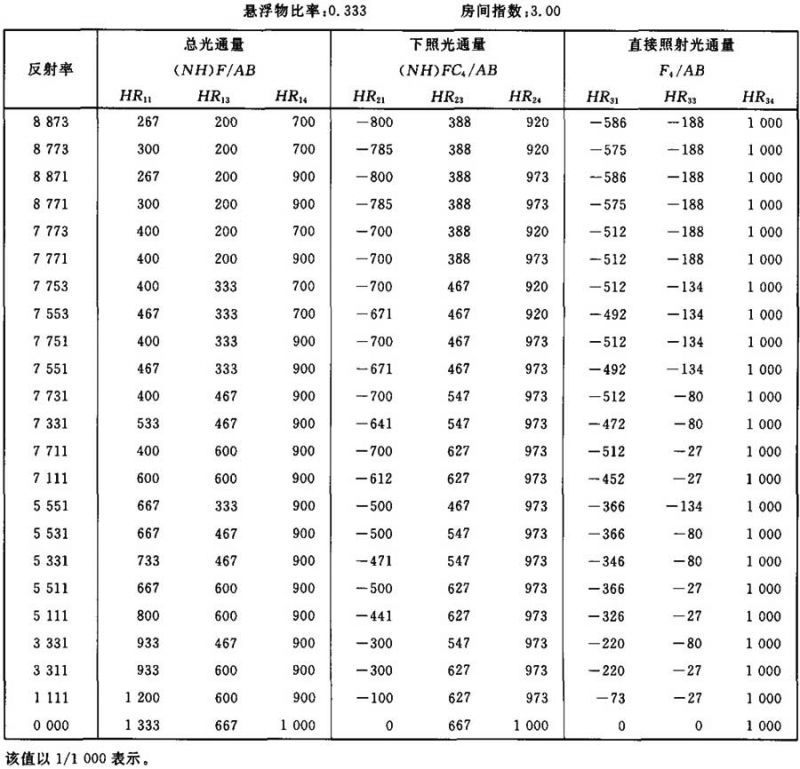
表Ⅲ.21
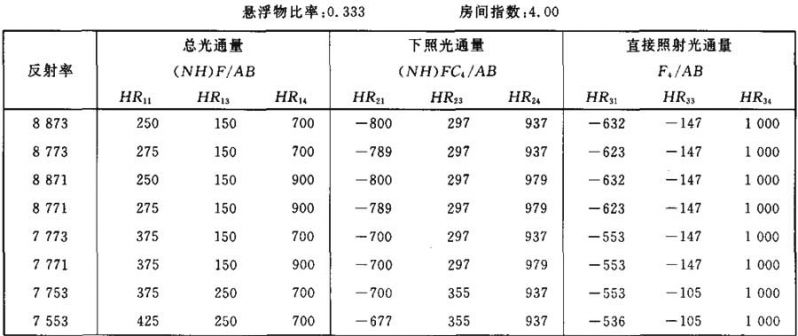
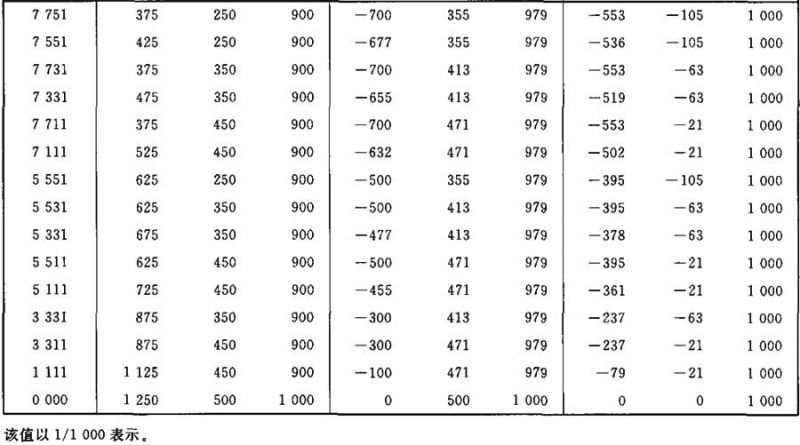
表Ⅲ.22
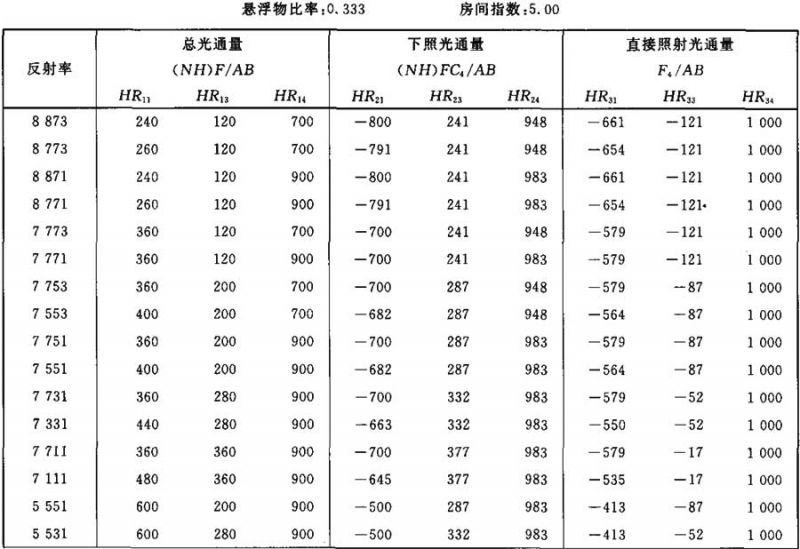
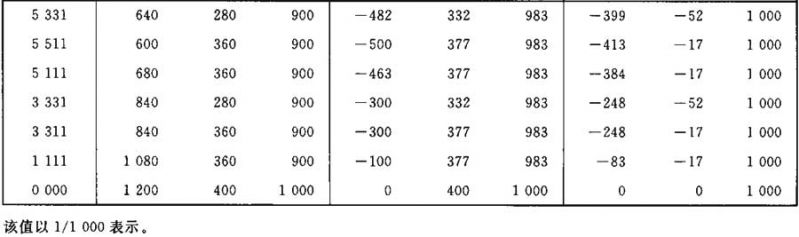
表Ⅲ.23
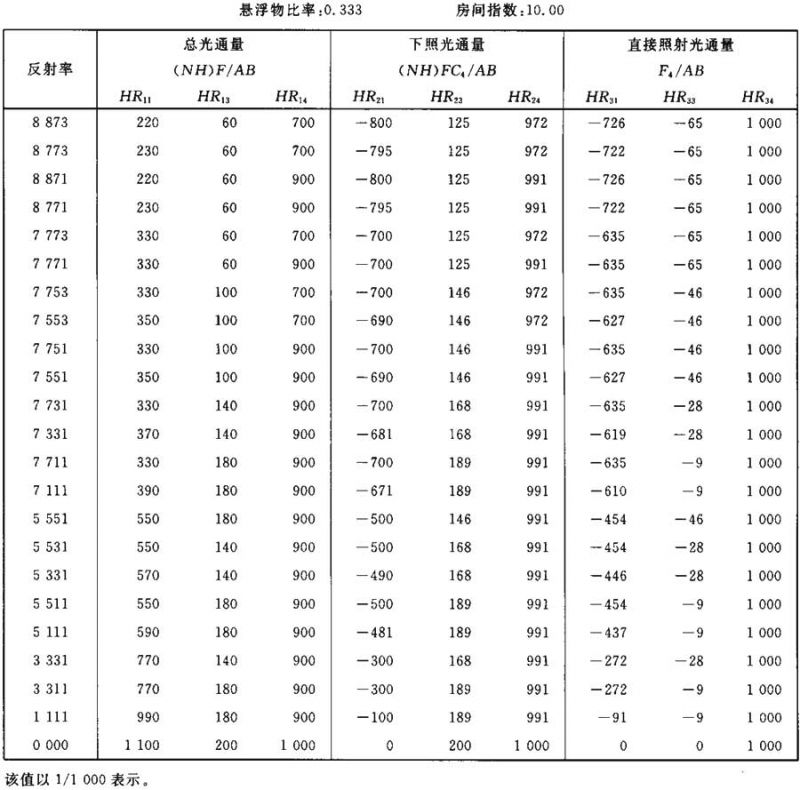
表Ⅲ.24
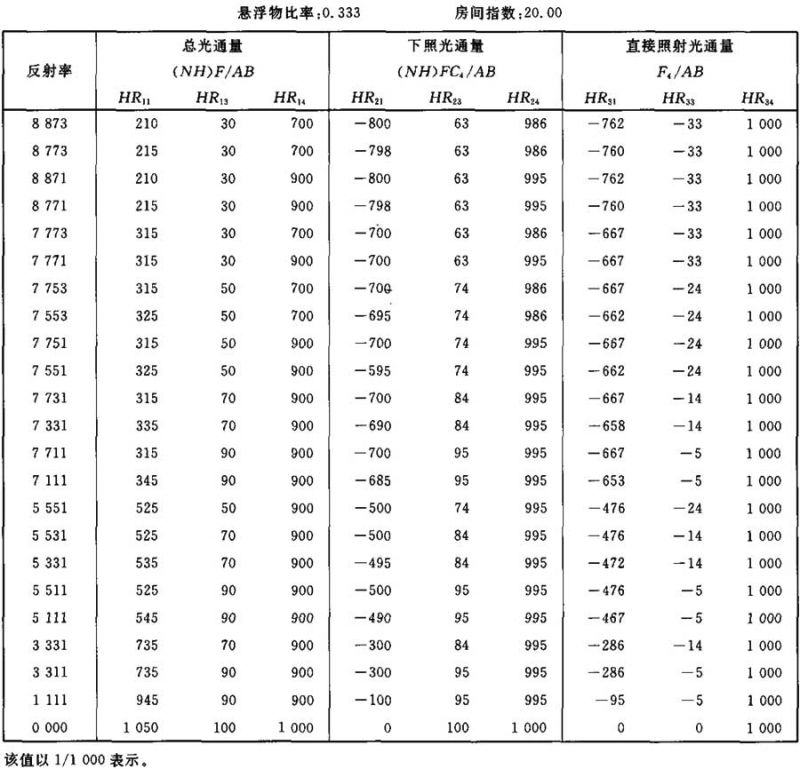
附录A 使用计算机的计算公式
A.1 工作面的直射光通量F4的计算

A.2 平均照度E1、E3和E4的计算
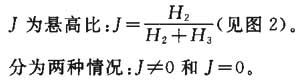
A.2.1 J≠0
(4)E=RM·FD,其中
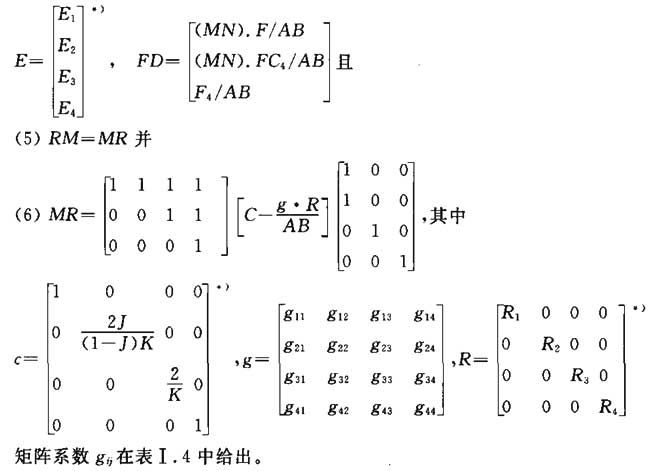
A.2.2 J=0
同样可使用公式(4),但矩阵MR可简化为:
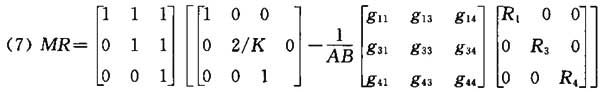
A.3 直射光通量的计算
A.2的公式适用于FD、MR和E。
A.4 交换系数的计算
边长为A和B,高度为H的长方体房间,两个平行面的交换系数gij由以下公式给出:

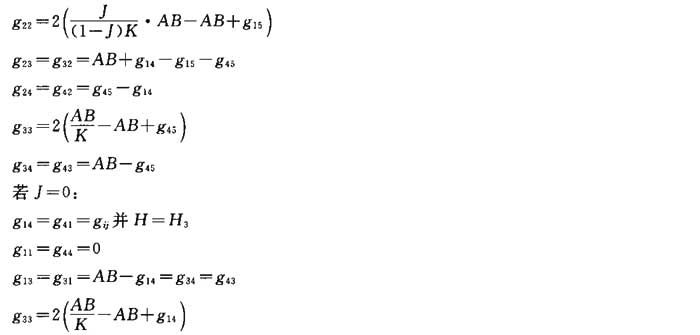
附录B 计算的数学背景
B.1 工作面上直接照射光通量的计算
假设灯具的光沿垂直轴呈锥形分布,下半球部分的光可近似用如下多项式表示:
(1)F=p1u+p2u2+p3u3+p4u4
其中
(2)u=1—cosγ=w/2π
w是圆锥形的立体角,γ是它的半顶角。
由此定义,灯具光强为:
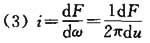
代入(1)和(3),逐步得出:
(4)i=q1+q2cosγ+q3cos2γ+q4cos3γ
(5)并q=D·p
q和P分别为qj和pj的列矩阵,D是附录A中公式2”给出的方矩阵。
多项式(4)可被解释为由各分量部分组成。
(6)i=1,i=cosγ,i=cos2γ,i=cos3γ
包含权重因子q1,q2,q3,q4
在矩形一角之上的高度为1,并且具有(6)式的光强分布的灯具所发出的到以A和B为边长的矩形内的光通量分别为Y1,Y2,Y3,Y4,可在附录A的公式(3)中得到。
灯具从相同位置向相同矩形发出的光通量fu:
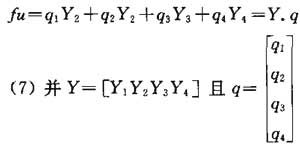
四个区域的光通量FC1,FC2,FC3,FC4为四个区域的数值u=1/4,2/4,3/4和4/4的F值。
代入式(1)中的四个数值,产生四个线性公式。
(8)FC=S·p
FC是累积区域光通量的列矩阵,S是附录A公式(2″′)中给出的矩阵,反向代入式(8),由公式(5)的得出:
(9)q=D·S-1·FC
代入式(7),导出
(10)fu=Y·q=y·D·S-1·FC
可写作:
(11)fu=GM1.FC1+GM2.FC2+GM3.FC3+GM4.FC4,
其中[GM1 GM2 GM3 GM4]=Y·D·S-1
系数GMj(几何乘数)仅由(X,Y,H)决定,而FCj只由灯具的光度分布决定。在表Ⅰ中可查到(乘以1000)。
B.2 互反射
根据此前结论,认为有四个面与互反射有关:天花板(1),中楣(2),墙面(3),和工作面(4)。
表面(j)接收到的总光通量Φj等于直接辐射到表面的总光通量Fj,以及由互反射产生的光通量IFj的和。

式中:
gji=gij=表面(i)和(j)间的交换系数;
Ri=表面(i)的反射率;
Ai=表面(i)的面积。
当式(13)代入式(12)时,结果见如下公式:
(14)Φ=F+g·R·A-1·Φ
式中:
Φ=列矩阵,系数Φj(j=1,2,3,4),
F=列矩阵,系数Fj(j=1,2,3,4),
g=(4,4)矩阵,系数gij(i=1,2,3,4 j=1,2,3,4),
R=4次对角矩阵,系数Ri(i=1,2,3,4)且
A=4次对角矩阵,系数Ai(i=1,2,3,4)
(14)式可重新整理如下:
(15)F=[1—g·R·A-1]·Φ
下面只考虑F12=F1+F2(F1与F2的和)的情况,而不单独考虑F1和F2,那么原来的四个直射光通量减少为三个直射光通量。
假设总光通量Φ12=Φ1+Φ2在表面(1)和表面(2)上均匀分布,意味着天花板照度E1和中楣照度E2相等:E1=E2。
以上内容通过数学方法表示为:


将(16)式代入(15)式,得出:
(18)F″=T[1—g·R·A-1]·Φ
注意到Φ=A·E′=A·U·E(18)也可写作
(19)F″=T[A—g·R]U·E
式中直射光通量的三个数值可以表示为三个平均照度。
代替这三个直射光通量,F12F3和F4线性组合也可以使用,例子如下:
F1′=F12+F3+F4=NM.F.为总光通量
F2′=F3+F4=NM.FC4为下照光通量
F3′=F4=∑fu为工作面的直射光通量
如果F′是系数F1′、F2′、F3′的列矩阵,F′可通过F″与V相乘得到:

矩阵A—g·R包含有区域的尺寸。为建立表格,更好的办法是使用数字。可通过将公式(21)两边分别除以区域值获得,例如A4区域工作面:
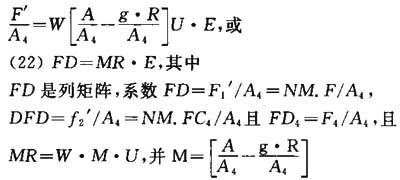
矩阵MR的系数在表Ⅲ中给出,从公式(22)得出:
(23)E=RM·FD其中RM=MR-1
矩阵RM的系数在表Ⅱ中给出。
B.3 交换系数
交换系数的定义参见国际照明词汇。
根据定义与互换法则得出:

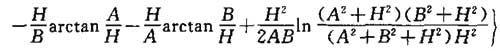
式中的A和B是表面的边长,H是表面之间的距离。
对于任意平面(i)遵从如下定义:
d)gii=0 (i=1.4)
当作为辅助平面(5)引入灯具平面时,辅助系数g15;和g45可通过上式计算出来。当观察以上四种表述时,要求的交换系数可作为g14,g15,g45,A1,A2,A3和A4的函数表示。
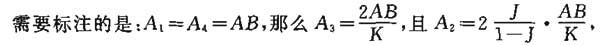
由此,交换系数可以作为g14,g15,g45,AB,J和K的函数表示。推导出的公式在A.4中给出。
下载地址
©版权声明
资源来自互联网,如有侵权请联系删除
