标准规范下载简介

在线阅读

中华人民共和国国家标准

优先数和优先数化整值系列的选用指南

Guide to the choice of series of preferred numbers and of series
containing more rounded values of preferred numbers
(ISO 497:1973,IDT)

GB/T 19764-2005

发布部门：中华人民共和国国家质量监督检验检疫总局
中国国家标准化管理委员会
发布日期：2005年05月16日
实施日期：2005年12月01日

前 言

    本标准等同采用国际标准ISO 497:1973《优先数和优先数化整值系列的选用指南》（英文版）。
    为便于使用，本标准对ISO 497做了下列编辑性修改：
    ——“本国际标准”一词改为“本标准”；
    ——删去了国际标准前言；
    ——按GB/T 1．1-2000《标准化工作导则 第1部分：标准的结构和编写规则》的要求进行编写。
    本标准的附录A是资料性附录。
    本标准由全国产品尺寸和几何技术规范标准化技术委员会提出并归口。
    本标准起草单位：机械科学研究院中机生产力促进中心、时代集团公司、哈尔滨量具刃具厂、北京计量检测科学研究院。
    本标准主要起草人：王欣玲、李晓沛、王忠滨、郎岩梅、吴迅。

1 范围

    本标准规定了允许使用的优先数唯一化整值，用修正量的大、小分为两个化整值系列。
    本标准叙述了应用这些化整值的条件和采用的结果。
    本标准给出了在优先数和各种化整值之间正确选用的规则。
    本标准适用于在考虑实际情况而不能采用优先数时，是对ISO 17关于数系选用和化整值应用条件的补充指导。

2 规范性引用文件

    下列文件中的条款通过本标准的引用而成为本标准的条款。凡是注日期的引用文件，其随后所有的修改单（不包括勘误的内容）或修订版均不适用于本标准，然而，鼓励根据本标准达成协议的各方研究是否可使用这些文件的最新版本。凡是不注日期的引用文件，其最新版本适用于本标准。
    GB/T 321 优先数和优先数系(ISO 3:1973,IDT)
    GB/T 19763 优先数和优先数系的应用指南(ISO 17:1973,IDT)

3 严格遵循优先数的优点

3．1 概述
    无论是在各种机械零件自身的标准化上，还是在产品结构的标准化上，当其功能特性系列也象每个零件的尺寸那样采用等比级数时，使用优先数系都有优越性。

3．2 最佳的级数
    从规律性的观点，以及通过插入中间值组成较密系列，以适应新的需要的可能性来说，优先数能保证得到最佳的级数。

3．3 广泛的适用性
    优先数提供了逻辑性最强的方法，能在给定的领域内（电动机的功率，泵的输出量等），前后衔接不间断地满足整个范围的需要。

3．4 使技术和商业计算简单化
    因为优先数的积和商按定义也是优先数，所以可用对数值或序号而不用优先数自身进行计算，尤其是当系列（尺寸、表记价格等）按同样比例相乘或相除时，使计算大为简化。

3．5 便于计量单位的换算
    当测量系列值为优先数，同时换算系数近似为优先数时，能很方便地换算成其他计量单位。

4 化整值的应用

4．1 概述
    化整值和化整值系列只在下列情况下才允许采用，并应优先采用第一化整值系列R＇r。

4．2 在某些应用场合，由于十分必要的理由而无法使用优先数：
    a) 当只需要整数的参数时，就不可能保留全部有效数字（例如：齿轮的齿数用32代替31．5）。
    b) 对需要用偶数、整倍数以及要求数值具有可分性或具有加法性质的项值，有时用化整值比较适宜，例如，包装中的组合尺寸和由模数的整倍数所构成的元件尺寸等。
    c) 在没有公差要求的场合，优先数的有效位数所表示的精度，既无实际意义，也不便于测量的，可用化整值系列。例如，照相机的曝光时间以1/30秒取代1/31．5秒，采用了R"10/3系列(1,1/2,1/4,1/8,1/15,1/30,1/60,1/125,……秒)。

4．3 受到现有配套产品限制的尺寸参数系列，如因涉及到很广泛的协作范围和已有的大量物质基础，不宜轻易改变时（例如，考虑到经济性，继续使用现有的工、量具），可采用化整值系列，例如，标准直径和标准长度系列。

4．4 由于十分重要的原因（见4．2），可以认为采用化整值是合适的。如果是考虑经济性和心理因素（愿意使用较简单形式表示的值，尤其是在书写或读用优先数表示的示值有困难时）^1），就不允许采用化整值。因为这是主观上的原因，可能千变万化，引起企业标准和国家标准的不统一，给国际间的技术交流和贸易往来造成极大影响。^2）
    由于国际标准及技术文件是以优先数为基础的，现行的国家标准也采用优先数，与国际标准取得一致，但化整值和非优先数的值则难于取得一致。
    如果把一些不能改变的现行系列值（如物理常数）引入标准中，即令这些数值近似于优先数或其化整值，都不应认为是优先数的一种应用方式。这些系列不可能具备优先数的全部性质，并且使用时也会有困难，尤其在3．5那样的计算中。这一点同样适用于目前还难于改变的现行系列值，如齿轮模数。
1) 另外，在有些场合对于带有加法性质的项值，化整值的使用是有效的（也有例外）。如R"系列至少在一限定的范围内提供了一个解决问题的办法，例如：

3+4=7, 3+5=8, 3+6=9,

3+7=10， 3.5+4.5=8， 7+7=14等。

2）采用既非优先数，也非化整值的特殊值，无论是为了与不符合优先数但又尚未废止的现行标准取得一致，或者是为了互换性而保持现有生产过程，或者是为了继续使用现有的工、量具，都会给国际标准的转化带来一定的困难，同时也会影响按等比级数系列制造机器。

5 选用规则和化整值系列表

5.1 选取一些数值以满足某种用途的特定要求时。
    5.1.1 按下列顺序选择合适的公比：

5—10—20—40

    5.1.2 选择具有合适的项值精度和公比均匀性的系列（见表1），即：
        a) 优先采用R优先数系自身（表1注c）；
        b) 如有充分的理由而完全不能采用优先数时，则用第一化整值系列R＇；
        c) 最后才用第二化整值系列R"（表1注a）。


5.2 在选取单个数值（例如样机规格的编制）时，应考虑该值以后可能是某种公比的系列中的一项，因此，可按5.1规定选取一个优先数。当优先数中没有合适值时，可选取化整值。

6 采用化整值的危害

6．1 在系列中如果有一个化整值，或者允许一个符合上述规则的特殊值存在，因为它们不是一个优先数，所以也不可能转换成一个具有较小公比的系列。

6．2 化整值系列分级的均匀性比优先数系列差，因为在某些区间R＇系列的相对误差可达2．94％，而R"系列甚至可达5．61％³⁾。

6．3 派生系列分级的均匀性比R＇或R"系列更差。假如对两相邻的项值作反向修整，例如一个向下而另一个向上：以R＇40/4系列(…1．05…)为例，在1．23和1．7之间的相对误差达1．26％+2．51％=3．77％，而原R＇40系列的最大相对误差仅为2．94％，因而破坏了优先数系均匀性的基本原则。

6．4 化整值的精确程度不如优先数高，实际上化整值精度的降低在R＇系列的值中可达2．51％，在R"系列的值中达到5．36％。⁴⁾
    而且，由于上述情况，当要借助表1中第5列所给的序号进行计算时，化整值就不能用于新产品设计4)。

6．5 为解决同一问题，如果都选用不同的化整值系列而不用优先数，则会对国际间标准化的协调带来很大困难4)。
3) 例如线性尺寸的化整值的相对误差为5％，则其他方面相应的相对误差为：
    对二次方大于10％（横截面积和螺栓强度，活塞横截面积和发动机功率）；
    对三次方大于15％（零件的质量，轴的挠度）；
    对四次方大于20％（弹簧刚度）；
    对五次方大于25％（惯性矩）。
4) 见4.4条的角注2)。

附录A

（资料性附录）

项值的精度和公比的均匀性

A．1 定义
    A．1．1 概述
        为了正确理解和合理选用化整值，首先应研究计算值，优先数和化整值相对于理论值的相对程度（通常称为项值的精度），以及研究相应系列的公比均匀性。
    A．1．2 等项值相对于理论值的精度⁵⁾可以表示为以百分比描述的相对关系，用项值与理论值的差与理论值之比的百分比表示。
        优先数的相对误差列于GB/T 321-2005表1的第8列，并在本标准的表1中第7列重复列出。化整值的相对误差列于本标准表1中第8～第10列。
    A．1．3 某系列公比在给定点的均匀性为该点的实际公比（相邻两项的比值）与理论公比之间的误差，以百分比表示⁶⁾。
        表明两相邻项间公比均匀性的该误差，可用表1中第7～第10列所给项值误差的简单代数减法求得（略去无穷小量）⁷⁾。
        R、R＇和R"各系列在不同点的公比最大均匀性见表1中第1～第4列的底栏。

A．2 最大允许的误差
    A．2．1 如果给定这样一个条件，即化整值对相应理论值的误差应比相邻项理论值的误差小，则该条件可用最大允许误差来表示，其值在公比 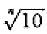不太大时可近似等于

    A．2．2 在极限情况下，两连续数之间的比值可能接近于1（即公比值），而这对系列的均匀性是不允许的。

A．3 计算值的实际误差
    在GB/T 321-2005表1的第7列中给出了计算值的五位有效数，它相对于理论值的最大误差≤0．00005，最大相对误差为0．0048％。

A．4 优先数的实际误差
    A．4．1 在GB/T 321-2005中给出了有三位有效数字的优先数，并在第8列中列出了优先数与计算值之间的相对误差。
    A．4．2 公比对误差不超过1．26％，而绝对误差有时是较大的；但要指出，由于按系列（即两项之间的公比）均匀性的原则选用了合适的圆整量，故使优先数的公比仍很接近理论公比（R40系列的最大不均匀性为1．15％）。

A．5 化整值的实际误差
    A．5．1 只有在特殊情况下才允许使用化整值，一般它仅有两位有效数字，有的甚至只有一位有效数字，然而在R＇和R"系列中仍保持了允许的精度和均匀性。⁸⁾
    A．5．2 化整值偏离理论值超过偏离优先数本身（见表1第7～第10列的框格中的最大误差）。R＇和R"系列的公比均匀性比优先数系列差很多，如R"5，最大不均匀性（见表1第1列～第4列最后一栏）达5．37％，而R5只有1．42％，R＇40达2．94％，而R40只有1．15％。
    A．5．3 应注意，在R"5或R"10中允许使用的化整值1．5，在更密的系列中不允许使用。因为1．5相对于理论值的误差为5．36％，它与连续项2．0间会引起5．60％的公比相对误差。这对公比约为1．25的R"10系列是允许的，因为按A．2．1R"10的最大允许误差为12．9％。然而1．5这个值确不能保留在公比约为1．12的R"20系列中，因为它对连续项1．8将造成6．58％公比相对误差，而R"20的最大允许误差仅为6．1％。
5) 例如对优先数8．5，略去计算值与理论值之间的差异，则其精度为：


6) 例如在R40系列中取1．60和1．70两项，该误差为：


7) 例如1．60和1．70两项的比值近似为：


    比值的精确值是1．0625，误差的精度值是0．00325或0．3％，因此精确到2/10000（就比例而言）。
8) 在1．18处R＇40使用的项值是1．2，它同理论值的误差为+0．97％，而1．18的误差为-0．71％，故它几乎与1．18一起被用；但从分级观点考虑，值1．2处于1．1和1．25之间是不太合适的，它与理论公比1．0593的误差可用A．1．2所述的第7列和第8列误差值的代数差计算，其结果为：


因此，这两连续公比分别以1．0886和1．0425代替理论值1．0593。

下载地址